
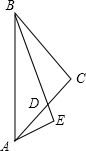
 如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,
如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,分析 (1)由BD平分∠ABC得到∠1=∠3,由于∠BDC=∠ADE,根据三角形内角和定理得到∠1=∠2,所以∠1=∠3,然后根据等角的余角相等即可得到∠ADE=∠BAE;
(2)延长AE交BC的延长线于F,如图,先证明△CBD≌△CAF,得到BD=AF,再利用等腰三角形的性质得到AE=EF,于是得到BD=2AE.
解答 (1)证明:∵BD平分∠ABC,
∴∠1=∠3,
∵AE⊥BD,
∴∠AEB=90°,
而∠BDC=∠ADE,
∴∠1=∠2,
∴∠1=∠3,
∴∠ADE=∠BAE;
(2)解:BD=2AE.理由如下:
延长AE交BC的延长线于F,如图,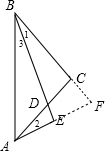 在△CBD和△CAF中,
在△CBD和△CAF中,
$\left\{\begin{array}{l}{∠1=∠2}\\{CB=CA}\\{∠BCD=∠ACF}\end{array}\right.$,
∴△CBD≌△CAF (ASA)
∴BD=AF,
∵BD平分∠ABC,BE⊥AF,
∴AE=EF,
∴BD=2AE.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了全等三角形的判定与性质和等腰三角形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
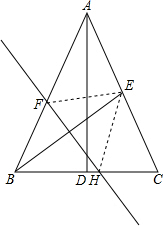 如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.
如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )
在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )| A. | 64个 | B. | 49个 | C. | 36个 | D. | 25个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
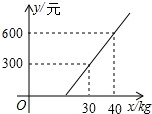 国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )| A. | 20kg | B. | 25kg | C. | 28kg | D. | 30kg |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com