
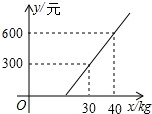
 国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )| A. | 20kg | B. | 25kg | C. | 28kg | D. | 30kg |
分析 设携带行李的重量x与其运费y(元)之间的函数关系式为y=kx+b,由待定系数法求出解析式,当y=0时求出x的值即可.
解答 解:设携带行李的重量x与其运费y(元)之间的函数关系式为y=kx+b,由题意,得
$\left\{\begin{array}{l}{30k+b=300}\\{40k+b=600}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=30}\\{b=-600}\end{array}\right.$,
∴y=30x-600.
当y=0时,30x-600=0,
∴x=20.
故选A.
点评 本题考查了与一次函数图象结合用一次函数解决实际问题,本题关键是理解一次函数图象的意义以及与实际问题的结合.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
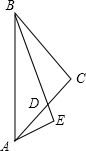 如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,
如图,△ABC中,BC=AC,∠ACB=90°,BD平分∠ABC,AE⊥BD,交BD延长线于E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形纸片ABCD中,AB=4cm,BC=8cm,现将A、C重合,使纸片折叠压平,设折痕为EF,
如图,矩形纸片ABCD中,AB=4cm,BC=8cm,现将A、C重合,使纸片折叠压平,设折痕为EF,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
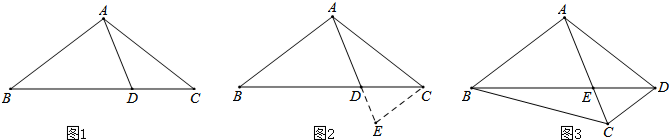
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
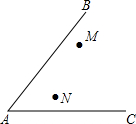 作图题:
作图题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
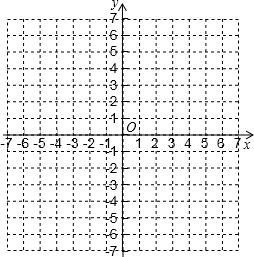 在如图所示的平面直角坐标系中表示下面各点:A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0).
在如图所示的平面直角坐标系中表示下面各点:A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com