
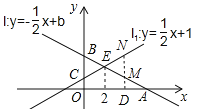
【题目】如图,已知直线![]() :
:![]() 与x轴,y轴的交点分别为A,B,直线
与x轴,y轴的交点分别为A,B,直线![]() :
: ![]() 与y轴交于点C,直线
与y轴交于点C,直线![]() 与直线
与直线![]() 的交点为E,且点E的横坐标为2.
的交点为E,且点E的横坐标为2.
(1)求实数b的值;
(2)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线![]() 与直线
与直线![]() 于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.
于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.

【答案】(1)3;(2)a=5或-1.
【解析】
(1)利用一次函数图象上点的坐标特征,由点E在直线![]() 上可得到点E的坐标,由点E在直线
上可得到点E的坐标,由点E在直线![]() 上,进而得出实数b的值;
上,进而得出实数b的值;
(2)依据题意可得MN=|1+![]() a(3
a(3![]() a)|=|a2|,BO=3.当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,即可得到|a-2|=3,进而得出a的值.
a)|=|a2|,BO=3.当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,即可得到|a-2|=3,进而得出a的值.
解:(1)∵点E在直线l1上,且点E的横坐标为2,
∴点E的坐标为(2,2),
∵点E在直线l上,
∴2=![]() ×2+b,
×2+b,
解得:b=3;
(2)如图,当x=a时,yM=3![]() a,yN=1+
a,yN=1+![]() a,
a,
∴MN=|1+![]() a(3
a(3![]() a)|=|a2|,
a)|=|a2|,
当x=0时,yB=3,
∴BO=3.
∵BO∥MN,
∴当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,
此时|a-2|=3,
解得:a=5或a=-1.
∴当以点B、O、M、N为顶点的四边形为平行四边形,a的值为5或-1.
故答案为:(1)3;(2)a=5或-1.


科目:初中数学 来源: 题型:
【题目】已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
(2)当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?
查看答案和解析>>
科目:初中数学 来源: 题型:
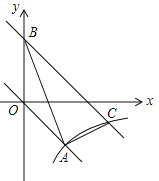
【题目】(2016四川省成都市)如图,在平面直角坐标xOy中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象都经过点A(2,﹣2).
的图象都经过点A(2,﹣2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于点B,与反比例函数图象在第四象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式2x+4y+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国七十周年,南岗区准备对某道路工程进行改造,若请甲工程队单独做此工程需4个月完成,若请乙工程队单独做此工程需6个月完成,若甲、乙两队合作2个月后,甲工程队到期撤离,则乙工程队再单独需几个月能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学著作《算术研究》一书中,对于任意实数,通常用x 表示不超过 x 的最大整数,如 3 , 2 2 , 2.1 3 。给出如下结论:①x x ;②若x n ,则 x 的取值范围是 n x n 1 ;③当1 x 1 时, 1 x 1 x 的值为 1 或 2;④ x 2.75 是方程 4x 2x 5 0 的唯一一个解。其中正确的结论有( )
A.①②B.②③C.①③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
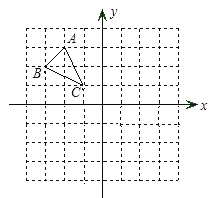
【题目】已知ABC 在平面直角坐标系中的位置如图(注: A、B、C 均在格点上)
(1)请在图中作出ABC 关于 y 轴对称的A1B1C1 ,并直接写出A1B1C1 顶点的坐标;
(2)求A1B1C1 的面积;
(3)再将A1B1C1 向下平移 4 个单位长度,得到A2 B2C2 ,若点 M m, n 是ABC 上一点,请直接写出 M 在A2 B2C2 上对应点 M 2 的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)+40+(﹣32)+(﹣8)
(2)12﹣(﹣18)+(﹣7)
(3)(+3![]() )﹣(﹣5
)﹣(﹣5![]() )+(﹣2
)+(﹣2![]() )﹣(﹣32
)﹣(﹣32![]() )
)
(4)81.26﹣293.8+8.74+111
查看答案和解析>>
科目:初中数学 来源: 题型:
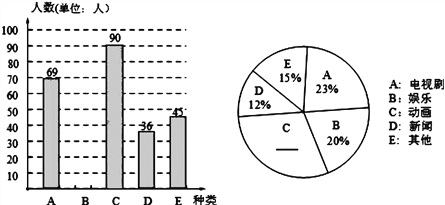
【题目】我市某中学为了了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有1500名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com