
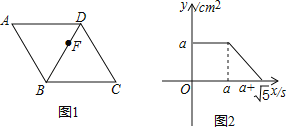
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
A. ![]() B. 2C.
B. 2C. ![]() D. 5
D. 5
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】小王、小张和小梅打算各自随机选择本周六的上午或下午去高邮湖的湖上花海去踏青郊游.
(1)小王和小张都在本周六上午去踏青郊游的概率为_______;
(2)求他们三人在同一个半天去踏青郊游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y=![]() x2﹣
x2﹣![]() x+3的绳子.
x+3的绳子.

(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的图象经过坐标原点
的图象经过坐标原点![]() ,且与
,且与![]() 轴另交点为
轴另交点为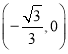 .
.
(1)求抛物线![]() 的解析式;
的解析式;
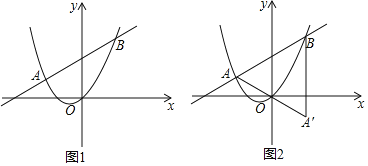
(2)如图![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() 和点
和点![]() (点
(点![]() 在第二象限),求
在第二象限),求![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
(3)在(2)中,若![]() ,设点
,设点![]() 是点
是点![]() 关于原点
关于原点![]() 的对称点,如图
的对称点,如图![]() .平面内是否存在点
.平面内是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
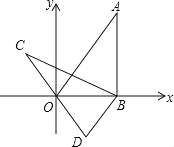
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).
(1)抛物线的对称轴为直线x=-3,AB=4.求抛物线的表达式;
(2)平移(1)中的抛物线,使平移后的抛物线经过点O,且与x正半轴交于点C,记平移后的抛物线顶点为P,若△OCP是等腰直角三角形,求点P的坐标;
(3)当m=4时,抛物线上有两点M(x1,y1)和N(x2,y2),若x1<2,x2>2,x1+x2>4,试判断y1与y2的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为原点,点
为原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .抛物线
.抛物线![]() 经过点
经过点![]() ,
,![]() ,与
,与![]() 交于点
交于点![]() .
.
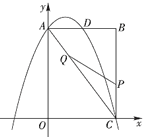
(1)求抛物线的函数解析式;
(2)![]() 为线段
为线段![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),
重合),![]() 为线段
为线段![]() 上一个动点,
上一个动点,![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
(3)在(2)的条件下,![]() 为抛物线
为抛物线![]() 的对称轴
的对称轴![]() 上一点,请求出使
上一点,请求出使![]() 为锐角三角形时,点
为锐角三角形时,点![]() 的纵坐标
的纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com