
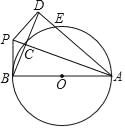
【题目】如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)判断PB与⊙O的位置关系,并说明理由;
(2)连接CE,若CE=3,AE=7,求⊙O的半径.
【答案】(1)PB与⊙O相切,理由见解析;(2)⊙O的半径为4.5.
【解析】
(1)根据线段垂直平分线的性质可得PB=PD,通过证明△ABP与△ADP全等,根据全等三角形对应角相等可得∠ABP=∠ADP=90°,再根据切线的判定定理即可得证;
(2)根据全等三角形的性质得∠BAC=∠DAC,得到BC=CE=3,然后证明△DCE与△DAB相似,然后根据相似三角形的对应边成比可推导得出DCDB=DEDA,代入相关数据即可求得答案.
(1)PB与⊙O相切,理由如下:
∵AB是⊙O的直径,
∴AC⊥BD,
又AB=AD,
∴AP是线段BD的垂直平分线,
∴PB=PD,
在△ABP和△ADP中,
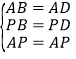 ,
,
∴△ABP≌△ADP(SSS),
∴∠ABP=∠ADP=90°,
∴PB与⊙O相切;
(2)∵△ABP≌△ADP,
∴∠BAC=∠DAC,
∴![]() ,
,
∴BC=CE=3,
∵AB=AD,AC⊥BD,
∴BC=CD=3,
∵四边形ABCE是⊙O的内接四边形,
∴∠DBA+∠CEA=180°,
∵∠DEC+∠CEA=180°,
∴∠DBA=∠DEC,
又∵∠CDE=∠ADB,
∴△DCE∽△DAB,
∴DC:DA=DE:DB,
∴DCDB=DEDA,即3×6=DE×(DE+7),
解得,DE=2,
∴DA=2+7=9,
∴AB=AD=9,
∴⊙O的半径为4.5.


科目:初中数学 来源: 题型:
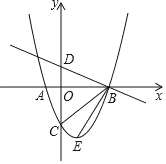
【题目】如图,抛物线y=ax2+bx﹣3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交子点C,且OB=OC=3OA,直线y=﹣![]() x+1与y轴交于点D.求∠DBC﹣∠CBE=_____.
x+1与y轴交于点D.求∠DBC﹣∠CBE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
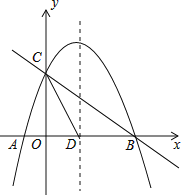
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知![]() ,
,![]() .
.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
![]() 点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
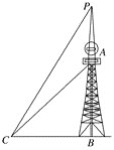
【题目】哈尔滨龙塔坐落于经济技术开发区,在钢结构塔中位居亚洲第一,世界第二.在塔上有一个室外观光平台A可以欣赏的哈尔滨市的全景,室外观光平台中央位置A距离塔顶P约146米,一名同学站在C处观察A点的仰角为45°,观察P点的仰角为60.5°,则龙塔PB的高度为______________.(已知:tan 60.5°=1.77)(精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() 此时可以得到数字密码171920.
此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
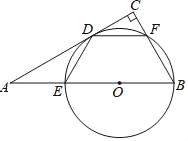
【题目】如图,点O是Rt△ABC的AB边上一点,∠ACB=90°,⊙O与AC相切于点D,与边AB,BC分别相交于点E,F.
(1)求证:DE=DF;
(2)当BC=3,sinA=![]() 时,求AE的长.
时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:sin30°=![]() ,tan30°=
,tan30°=![]() ,sin45°=
,sin45°=![]() ,tan45°=1,sin60°=
,tan45°=1,sin60°=![]() ,tan60°=
,tan60°=![]() ,由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
,由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,一辆小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?______;(填“是”或“否”)请简述你的理由_______.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是![]()
![]()
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com