
【题目】在平面直角坐标系中,点![]() 与
与![]()
![]() 称为一对泛对称点.
称为一对泛对称点.
(1)若点![]() ,
,![]() 是一对泛对称点,求
是一对泛对称点,求![]() 的值;
的值;
(2)若![]() ,
,![]() 是第一象限的一对泛对称点,过点
是第一象限的一对泛对称点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,线段
,线段![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,判断直线
,判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)抛物线![]()
![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交此抛物线于点
轴的平行线交此抛物线于点![]() (不与点
(不与点![]() 重合),过点
重合),过点![]() 的直线
的直线![]() 与此抛物线交于另一点
与此抛物线交于另一点![]() .对于任意满足条件的实数
.对于任意满足条件的实数![]() ,是否都存在
,是否都存在![]() ,
,![]() 是一对泛对称点的情形?若是,请说明理由,并对所有的泛对称点
是一对泛对称点的情形?若是,请说明理由,并对所有的泛对称点![]() ,
,![]() 探究当
探究当![]() >
>![]() 时
时![]() 的取值范围;若不是,请说明理由.
的取值范围;若不是,请说明理由.
【答案】(1)![]() ;(2)AB∥PQ,见解析;(3)对于任意满足条件的实数b,都存在M,N是一对泛对称点的情形,此时对于所有的泛对称点M(xM,yM),N(xN,yN),当yM>yN时,xM的取值范围是xM<1且xM≠0
;(2)AB∥PQ,见解析;(3)对于任意满足条件的实数b,都存在M,N是一对泛对称点的情形,此时对于所有的泛对称点M(xM,yM),N(xN,yN),当yM>yN时,xM的取值范围是xM<1且xM≠0
【解析】
(1)利用泛对称点得定义求出t的值,即可求出a.
(2)设P,Q两点的坐标分别为P(p,tq),Q(q,tp),根据题干条件得到A(p,0),B(0,tp),C(p,tp)的坐标,利用二元一次方程组证出k1=k2,所以AB∥PQ.
(3)由二次函数与x轴交点的特征,得到D点的坐标;然后利用二次函数与一元二次方程的关系,使用求根公式即可得到答案.
(1)解:因为点(1,2),(3,a)是一对泛对称点,
设3t=2
解得t=![]()
所以a=t×1=![]()
(2)解:设P,Q两点的坐标分别为P(p,tq),Q(q,tp),其中0<p<q,t>0.
因为PA⊥x轴于点A,QB⊥y轴于点B,线段PA,QB交于点C,
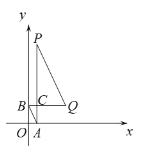
所以点A,B,C的坐标分别为:A(p,0),B(0,tp),C(p,tp)
设直线AB,PQ的解析式分别为:y=k1x+b1,y=k2x+b2,其中k1k2≠0.
分别将点A(p,0),B(0,tp)代入y=k1x+b1,得
 . 解得
. 解得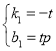
分别将点P(p,tq),Q(q,tp)代入y=k2x+b2,得
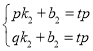 . 解得
. 解得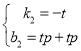
所以k1=k2.
所以AB∥PQ
(3)解:因为抛物线y=ax2+bx+c(a<0)交y轴于点D,
所以点D的坐标为(0,c).
因为DM∥x轴,
所以点M的坐标为(xM,c),又因为点M在抛物线y=ax2+bx+c(a<0)上.
可得axM 2+bxM+c=c,即xM(axM+b)=0.
解得xM=0或xM=-![]() .
.
因为点M不与点D重合,即xM≠0
所以点M的坐标为(-![]() ,c)
,c)
因为直线y=ax+m经过点M,
将点M(-![]() ,c)代入直线y=ax+m可得,a·(-
,c)代入直线y=ax+m可得,a·(-![]() )+m=c.
)+m=c.
化简得m=b+c
所以直线解析式为:y=ax+b+c.
因为抛物线y=ax2+bx+c与直线y=ax+b+c交于另一点N,
由ax2+bx+c=ax+b+c,可得ax2+(b-a)x-b=0.
因为△=(b-a)2+4ab=(a+b)2,
解得x1=-![]() ,x2=1.
,x2=1.
即xM=-![]() ,xN=1,且-
,xN=1,且-![]() ≠1,也即a+b≠0.
≠1,也即a+b≠0.
所以点N的坐标为(1,a+b+c)
要使M(-![]() ,c)与N(1,a+b+c)是一对泛对称点,
,c)与N(1,a+b+c)是一对泛对称点,
则需c=t ×1且a+b+c=t ×(-![]() ).
).
也即a+b+c=(-![]() )·c
)·c
也即(a+b)·a=-(a+b)·c.
因为a+b≠0,
所以当a=-c时,M,N是一对泛对称点.
因此对于任意满足条件的实数b,都存在M,N是一对泛对称点的情形.
此时点M的坐标为(-![]() ,-a),点N的坐标为(1,b).
,-a),点N的坐标为(1,b).
所以M,N两点都在函数y=![]() (b≠0)的图象上.
(b≠0)的图象上.
因为a<0,
所以当b>0时,点M,N都在第一象限,此时 y随x的增大而减小,所以当yM>yN时,0<xM<1;
当b<0时,点M在第二象限,点N在第四象限,满足yM>yN,此时xM<0.
综上,对于任意满足条件的实数b,都存在M,N是一对泛对称点的情形,此时对于所有的泛对称点M(xM,yM),N(xN,yN),当yM>yN时,xM的取值范围是xM<1且/span>xM≠0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点.连接MF,则△AOE与△BMF的面积比为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图AB是圆O的直径,射线AM⊥AB于点A.点D在AM上,连接OD交圆O于点E,过点D作DC=DA.交圆O于点C(A,C不重合),连接BC,CE.
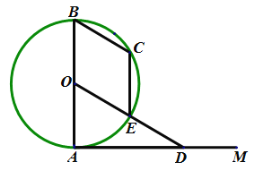
(1)求证:CD是圆O的切线;
(2)若四边形OECB是菱形,圆O的直径AB=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某品牌台灯竖直摆放在水平桌面上的侧面示意图,其中![]() 为桌面(台灯底座的厚度忽略不计),台灯支架
为桌面(台灯底座的厚度忽略不计),台灯支架![]() 与灯管
与灯管![]() 的长度都为
的长度都为![]() ,且夹角为
,且夹角为![]() (即
(即![]() ),若保持该夹角不变,当支架
),若保持该夹角不变,当支架![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 时,支架与灯管落在
时,支架与灯管落在![]() 位置(如图2所示),则灯管末梢
位置(如图2所示),则灯管末梢![]() 的高度会降低_______
的高度会降低_______![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,由于四边形具有不稳定性,因此在同一平面推矩形的边可以改变它的形状(推移过程中边的长度保持不变).已知矩形ABCD,AB=4cm,AD=3cm,固定边AB,推边AD,使得点D落在点E处,点C落在点F处.
(1)如图2,如果∠DAE=30°,求点E到边AB的距离;
(2)如图3,如果点A、E、C三点在同一直线上,求四边形ABFE的面积.
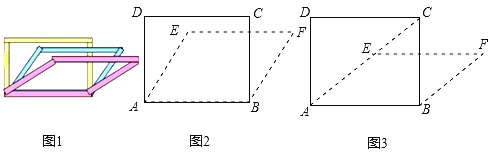
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
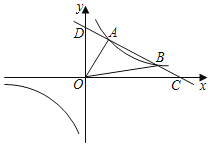
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今很多初中生喜欢购头饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题
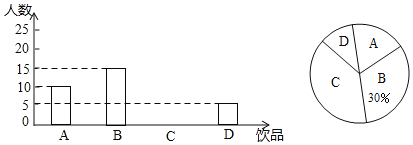
(1)这个班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称 | 白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格(元/瓶) | 0 | 2 | 3 | 4 |
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名班委干部(其中有两位班长记为A,B,其余三位记为C,D,E)中随机抽取2名班委干部作良好习惯监督员,请用列表法或画树状图的方法求出恰好抽到2名班长的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为进一步推进“一校一球队、一级一专项、一人一技能”的体育活动,决定对学生感兴趣的球类项目(A:足球,B:篮球,C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).
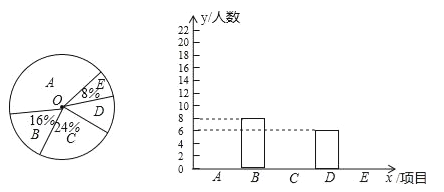
(1)该班对足球和排球感兴趣的人数分别是 、 ;
(2)若该校共有学生3500名,请估计有多少人选修足球?
(3)该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com