
【题目】在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则称这个点为“美好点”,如图,过点P分别作x轴,y轴的垂线,与坐标轴围成的矩形OAPB的周长与面积相等,则P为“美好点”.

(1)在点M(2,2),N(4,4),Q(﹣6,3)中,是“美好点”的有 ;
(2)若“美好点”P(a,﹣3)在直线y=x+b(b为常数)上,求a和b的值;
(3)若“美好点”P恰好在抛物线y=![]() x2第一象限的图象上,在x轴上是否存在一点Q使得△POQ为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
x2第一象限的图象上,在x轴上是否存在一点Q使得△POQ为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)N、Q;(2)a=6,b=﹣9或a=﹣6,b=3;(3)存在,点Q的坐标为(6,0)或(![]() ,0).
,0).
【解析】
(1)根据“美好点”的定义逐个验证即可;
(2)对于P点,对应图形的周长为:2×(|a|+3)=2|a|+6,面积为3|a|,因为点P是“美好点”,故2|a|+6=3|a|,即可求解;
(3)根据点P是“美好点”确定点P的坐标,设点Q的坐标为(x,0),再分以下三种情况:当∠POQ=90°时,此种情况不存在;当∠PQO=90°时,则PO2=PQ2+OQ2;当∠OPQ=90°时,则OQ2=PQ2+OP2,分别列出关于x的方程,解得x即可.
解:(1)对于M点,对应图形的周长为:2×(2+2)=8,面积为2×2=4≠8,故点M不是“美好点”;
对于点N,对应图形的周长为:2×(4+4)=16,面积为4×4=16,故点N是“美好点”;
对于点Q,对应图形的周长为:2×(6+3)=18,面积为6×3=18,故点Q是“美好点”;
故答案为:N、Q;
(2)对于P点,对应图形的周长为2×(|a|+3)=2|a|+6,面积为3|a|,
∵点P是“美好点”,
∴2|a|+6=3|a|,解得:a=±6,
将P(a,﹣3)代入y=x+b得:﹣3=a+b,则b=﹣3﹣a,
∴当a=6时,b=-9;当a=-6时,b=3,
故a=6,b=﹣9或a=﹣6,b=3;
(3)存在,理由如下:
设点P的坐标为(m,n),则n=![]() m2(m>0,n>0),
m2(m>0,n>0),
由题意得:2m+2n=mn,∴2m+![]() m2=
m2=![]() m3,
m3,
解得:m=6或﹣4(舍去)或0(舍去),
故点P的坐标为(6,3);
设点Q的坐标为(x,0),
则PQ2=(x﹣6)2+32=(x﹣6)2+9,
PO2=36+9=45,
OQ2=x2,
当∠POQ=90°时,∵点Q在x轴上,则∠POQ≠90°,此种情况不存在;
当∠PQO=90°时,则PO2=PQ2+OQ2,∴45=(x﹣6)2+9+ x2,解得x=6或x=0(舍去);
当∠OPQ=90°时,则OQ2=PQ2+OP2,∴x2=(x﹣6)2+9+45,解得x=![]() ;
;
综上所述,符合条件的点Q的坐标为:(6,0)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______________________;
(Ⅱ)解不等式②,得____________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两点的坐标分别为(﹣4,0),(0,4),C、F分别是直线x=6和x轴上的动点,CF=12,D是CF的中点,连接AD交y轴与点E,△ABE面积的最小值为_____cm.
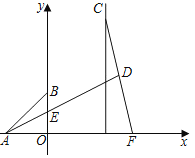
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知Rt△ABC中,∠B=90°,BC=4,AB=4,现将△ABC沿BC方向平移到△A′B′C′的位置.若平移的距离为3,则△ABC与△A′B′C′重叠部分的阴影面积为__.
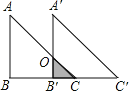
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=![]() m与y轴交于点C,与x轴交于点A和点B(其中点A在y轴左侧,点B在y轴右侧).
m与y轴交于点C,与x轴交于点A和点B(其中点A在y轴左侧,点B在y轴右侧).
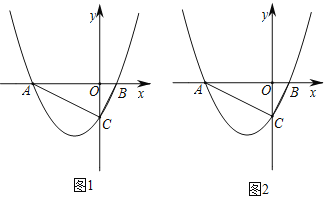
(1)若抛物线y=![]() m的对称轴为直线x=1,求抛物线的解析式;
m的对称轴为直线x=1,求抛物线的解析式;
(2)如图1,∠ACB=90°,点P是抛物线y=![]() m上的一点,若S△BCP=
m上的一点,若S△BCP=![]() ,求点P的坐标;
,求点P的坐标;
(3)如图2,过点A作AD∥BC交抛物线于点D,若点D的纵坐标为﹣![]() m,求直线AD的解析式.
m,求直线AD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和图形
和图形![]() ,给出如下定义:若图形
,给出如下定义:若图形![]() 上存在两个点
上存在两个点![]() ,使得
,使得![]() 是边长为2的等边三角形,则称点
是边长为2的等边三角形,则称点![]() 是图形
是图形![]() 的一个“和谐点”.
的一个“和谐点”.
已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 的半径为
的半径为![]() .
.
(1)若![]() ,在点
,在点![]() 中,直线
中,直线![]() 的和谐点是___________;
的和谐点是___________;
(2)若![]() 上恰好存在2个直线
上恰好存在2个直线![]() 的和谐点,求
的和谐点,求![]() 的取值范围;
的取值范围;
(3)若![]() ,线段
,线段![]() 上存在
上存在![]() 的和谐点,直接写出
的和谐点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州融创乐园是国内首个以南越文化、岭南风格为主题的游乐园,自2019年6月开园以来受到了国内外游客的热捧.某旅游团组织一批游客游玩了乐园内的四个网红项目,“A.双龙飞舞”、“B.飞跃广东”、“C.云霄塔”、“D.怒海狂涛”,并进行了“我最喜欢的一个项目”的投票评选活动,投票结果绘制成以下两幅尚未完整的统计图.请你根据图中提供的信息,解答下列问题:
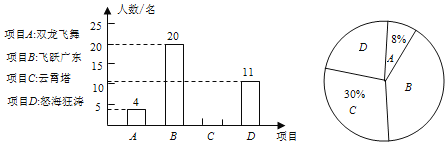
(1)参与投票的游客总人数为 人;
(2)扇形统计图中B所对的圆心角度数为 度,并补全条形统计图;
(3)从投票给“双龙飞舞“的3名男生和1名女生中随机抽取2名了解情况,请你用列举法求恰好抽到1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com