练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

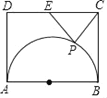
    【题目】我们发现：若AD是△ABC的中线，则有AB2+AC2＝2（AD2+BD2），请利用结论解决问题：如图，在矩形ABCD中，已知AB＝20，AD＝12，E是DC中点，点P在以AB为直径的半圆上运动，则CP2+EP2的最小值是_____．

    【答案】108

    【解析】

    设点O为AB的中点，连接EO交半圆于点P，此时PE取最小值，利用矩形的性质可求出EC、EP的值，则CP2+EP2＝2PE2+CE2，代入数值即可求出结论．

    解：设点O为AB的中点，连接EO交半圆于点P，此时PE取最小值，

    ∵AB＝20，四边形ABCD为矩形，

    ∴CD＝AB，EO＝AD，

    ∴OP＝CE＝AB＝10，

    ∴EP＝OE﹣OP＝AD﹣OP＝2，

    ∴CP2+EP2＝2PE2+CE2＝2×22+102＝108．

    故答案为：108．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

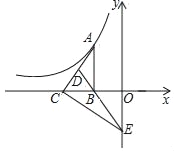
    【题目】如图，Rt△ABC的直角边BC在x轴负半轴上，斜边AC上的中线BD的反向延长线交y轴负半轴于点E，反比例函数y＝﹣（x＜0）的图象过点A，则△BEC的面积是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求函数的最值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

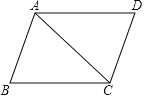
    【题目】如图，四边形ABCD 是平行四边形，AB＝c，AC＝b，BC＝a，抛物线 y＝ax2+bx﹣c 与 x 轴的一个交点为（m，0）．

    （1）若四边形ABCD是正方形，求抛物线y＝ax2+bx﹣c的对称轴；

    （2）若 m＝c，ac﹣4b＜0，且 a，b，c为整数，求四边形 ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

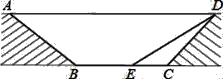
    【题目】为缓解交通拥堵，某区拟计划修建一地下通道，该通道一部分的截面如图所示（图中地面AD与通道BC平行，通道水平宽度BC为8米，∠BCD=135°，通道斜面CD的长为6米，通道斜面AB的坡度i=1：．

    （1）求通道斜面AB的长；

    （2）为增加市民行走的舒适度，拟将设计图中的通道斜面CD的坡度变缓，修改后的通道斜面DE的坡角为30°，求此时BE的长．

    （答案均精确到0.1米，参考数据：≈1.41，≈2.24，≈2.45）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场以每件42元的价格购进一种服装,由试销知,每天的销量t与每件的销售价x(元）之间的函数关系为t=204-3x。

    （1）试写出每天销售这种服装的毛利润y(元）与每件销售价x(元）之间的函数表达式（毛利润=销售价-进货价）； 并求出自变量的取值范围。

    （2）每件销售价为多少元，才能使每天的毛利润最大？最大毛利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D．过点C作CF∥AB，在CF上取一点E，使DE=CD，连接AE．对于下列结论：①AD=DC；②△CBA∽△CDE；③=；④AE为⊙O的切线，一定正确的结论全部包含其中的选项是（ ）

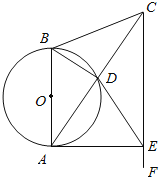
    A. ①② B. ①②③ C. ①④ D. ①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】作出反比例函数y＝－的图象，并结合图象回答：(1)当x＝2时，y的值；(2)当1＜x≤4时，y的取值范围；(3)当1≤y＜4时，x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ABC=90°，tan∠BAC=2，A（0，a），B（b，0），点C在第二象限，BC与y轴交于点D（0，c），若y轴平分∠BAC，则点C的坐标不能表示为（　　）

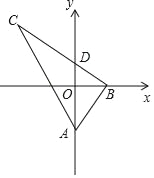
    A. （b+2a，2b） B. （﹣b﹣2c，2b）

    C. （﹣b﹣c，﹣2a﹣2c） D. （a﹣c，﹣2a﹣2c）

    查看答案和解析>>

    同步练习册答案