
| A、1 | B、2 | C、3 | D、4 |
科目:初中数学 来源: 题型:
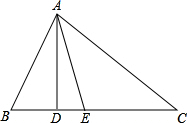 如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC.
如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC.| ∠B的度数 | ∠C的度数 | ∠DAE的度数 |
| 70° | 30° | (此格不需填写) |
| 65° | 25° | |
| 50° | 20° | |
| 80° | 56° |
查看答案和解析>>
科目:初中数学 来源: 题型:
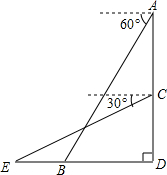 小明在大楼顶部A处测得小亮所在地B处的俯角为60°,当小明下午到大楼的C处时,发现小亮在俯角为30°的E处,E在直线BD上,已知BE=10米,AC=30米,问大楼高多少米?(结果精确到0.1米,
小明在大楼顶部A处测得小亮所在地B处的俯角为60°,当小明下午到大楼的C处时,发现小亮在俯角为30°的E处,E在直线BD上,已知BE=10米,AC=30米,问大楼高多少米?(结果精确到0.1米,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、等边对等角 |
| B、周长相等的两个等腰三角形全等 |
| C、等腰三角形的角平分线、中线和高线互相重合 |
| D、三角形一条边的两个顶点到这条边上的中线所在直线的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
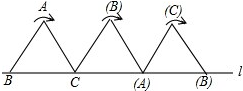 将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )
将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )A、
| ||
B、(2+
| ||
| C、πcm | ||
D、2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
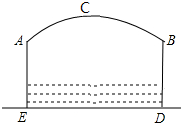 如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m.试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m.试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com