
【题目】在抗洪抢险中,人民解放军的冲锋舟沿东西方向的河流抢救灾民,早晨从![]() 地出发,晚上最后到达
地出发,晚上最后到达![]() 地,约定向东为正方向,当天航行依次记录如下(单位:千米)
地,约定向东为正方向,当天航行依次记录如下(单位:千米)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,问:
,问:
(1)![]() 地在
地在![]() 地的东面,还是西面?与
地的东面,还是西面?与![]() 地相距多少千米?
地相距多少千米?
(2)这一天冲锋舟离![]() 最远多少千米?
最远多少千米?
(3)若冲锋舟每千米耗油![]() 升,邮箱容量为
升,邮箱容量为![]() 升,求途中至少需要补充多少升油?
升,求途中至少需要补充多少升油?
【答案】(1)B地在A地东面,与![]() 地相距28千米;(2)这一天冲锋舟离
地相距28千米;(2)这一天冲锋舟离![]() 最远距离是
最远距离是![]() 千米;(3)途中至少需要补充
千米;(3)途中至少需要补充![]() 升;
升;
【解析】
(1)根据有理数的加法运算,可得答案;
(2)根据有理数的加法,可得每次行驶距A地的距离,根据有理数的大小比较,可得答案;
(3)根据有理数的加法,可得行驶总距离,根据行驶总距离乘以单位耗油量,可得答案。
(1)由题意得![]() (千米).
(千米).
答:B地在A地东面,与![]() 地相距28千米;
地相距28千米;
(2)第一次距A第14千米,
第二次距A地![]() (千米),
(千米),
第三次距A地![]() (千米),
(千米),
第四次距A地![]() (千米),
(千米),
第五次距A地![]() (千米),
(千米),
第六次距A地![]() (千米),
(千米),
第七次距A地![]() (千米),
(千米),
第八次距A地![]() (千米),
(千米),![]() >
>![]() >
>![]() >
>![]() >
>![]() >
>![]() .
.
答:这一天冲锋舟离![]() 最远距离是
最远距离是![]() 千米.
千米.
(3)![]() (升).
(升).
途中至少需要补充![]() (升).
(升).
答:途中至少需要补充![]() 升;
升;


科目:初中数学 来源: 题型:
【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.
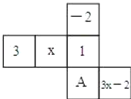
(1)求x的值.
(2)求正方体的上面和底面的数字和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:求若干个相同的有理数(均不等于 ![]() )的除法运算叫做除方,如
)的除法运算叫做除方,如 ![]() ,
, ![]() 等,类比有理数乘方,我们把
等,类比有理数乘方,我们把 ![]() 记作
记作 ![]() ,读作“
,读作“ ![]() 的圈
的圈 ![]() 次方,”
次方,” ![]() 记作
记作 ![]() ,读作:“
,读作:“ ![]() 的圈
的圈 ![]() 次方”.一般地,把
次方”.一般地,把 ![]() 记作a , 读作“
记作a , 读作“ ![]() 的圈
的圈 ![]() 次方”
次方”
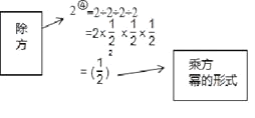
(1)(初步探究)
Ⅰ.直接写出计算结果: ![]() =________,
=________, ![]() ________.
________.
Ⅱ.关于除方,下列说法错误的是(________)
A.任何非零数的圈 ![]() 次方都等于它的倒数
次方都等于它的倒数
B.两个数互为倒数,那么它的n次方和圈n次方也互为倒数
C.对于任何正整数 ![]() ,(-1)=1
,(-1)=1
D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
(2)(深入思考)
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
Ⅰ.试一试,仿照上面的算式,将下列运算结果直接写成幂的形式.- ![]() ________;
________;![]() ________.
________.
Ⅱ.想一想:将一个非零有理数 ![]() 的圈 /span>
的圈 /span>![]() 次方写成幂的形式等于________.
次方写成幂的形式等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
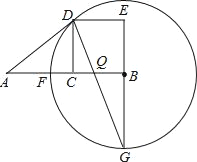
【题目】设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.
求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CFEG.
查看答案和解析>>
科目:初中数学 来源: 题型:
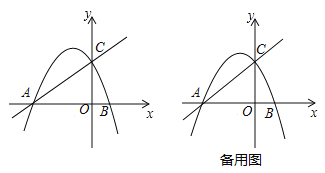
【题目】在直角坐标平面内,直线y=![]() x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣![]() +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
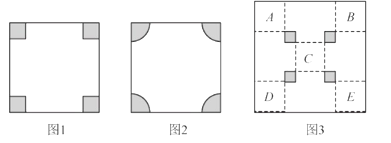
【题目】(1)探索:如图1,在边长为![]() 的正方形纸片的4个角都剪去1个边长是
的正方形纸片的4个角都剪去1个边长是![]() 的正方形.试用含
的正方形.试用含![]() 的式子表示纸片剩余部分的面积为_______________________;
的式子表示纸片剩余部分的面积为_______________________;
(2)变式:如图2,在边长为![]() 的正方形纸片的4个角都剪去一个相同的扇形,扇形的半径为
的正方形纸片的4个角都剪去一个相同的扇形,扇形的半径为![]() ,用
,用![]() 表示纸片剩余部分面积为______________________,剩余部分图形的周长为_____________________;
表示纸片剩余部分面积为______________________,剩余部分图形的周长为_____________________;
(3)拓展:世博会中国国家馆模型的平面图如图3所示,其外框是一个大正方形,中间四个全等的小正方形(阴影部分)是支撑展馆的核心筒,标记字母的五个全等的正方形是展厅,展厅的边长为![]() ,已知核心筒的边长比展厅的边长的一半多1米,用含有
,已知核心筒的边长比展厅的边长的一半多1米,用含有![]() 的式子表示外框的边长
的式子表示外框的边长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动互联网是现代通信平台,可以实现手机之间的私密互联,任意两台手机私密互联构成一条连接通路.
(1)若![]() 台手机
台手机![]() 、
、![]() 、
、![]() 同时私密互联,请画出图形,并用线段表示构成的所有连接通路:
同时私密互联,请画出图形,并用线段表示构成的所有连接通路:
(2)若![]() 台手机
台手机![]() 、
、![]() 、
、![]() 、
、![]() 同时私密互联,形成几条连接通路?
同时私密互联,形成几条连接通路?
(3)若![]() 台手机同时私密互联,形成几条连接通路?请用含
台手机同时私密互联,形成几条连接通路?请用含![]() 的式子表示.
的式子表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,相距5km的A、B两地间有一条笔直的马路,C地位于AB两地之间且距A地2km,小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动,当到达B地后立即以原来的速度返回。到达A地停止运动,设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点,以从A到B为正方向,用1个单位长度表示1km,解答下列各问:
![]()
(1)指出点A所表示的有理数;
(2)求t =0.5时,点P表示的有理数;
(3)当小明距离C地1km时,直接写出所有满足条件的t值;
(4)在整个运动过程中,求点P与点A的距离(用含t的代数式表示);
(5)用含t的代数式表示点P表示的有理数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com