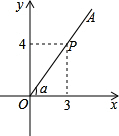练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．如图，P是∠α的边OA上一点，且P点的坐标为（3，4），则sin（90°-α）=$\frac{3}{5}$．

    分析 根据勾股定理，可得OP的长，根据一个角的余弦等于它余角的正弦，可得答案．

    解答 解：由勾股定理，得
    OP=$\sqrt{{3}^{2}+{4}^{2}}$=5．
    由一个角的余弦等于它余角的正弦，得
    sin（90°-α）=cosα=$\frac{3}{5}$，
    故答案为：$\frac{3}{5}$．

    点评 本题考查了锐角三角函数的定义，利用了互余两角三角函数的关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．如图，在△ABC中，∠ABC=45°，AC=5，F是高AD和BE的交点，则BF的长是（　　）
    A．7B．6C．5D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．使代数式$\frac{3}{2x-3}$有意义的x的取值范围是（　　）
    A．x＜$\frac{3}{2}$B．x=$\frac{3}{2}$C．x＞$\frac{3}{2}$D．x≠$\frac{3}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．$\sqrt{（\sqrt{2015}-50）^{2}}$的值等于（　　）
    A．±（$\sqrt{2015}$-50）B．$\sqrt{2015}$±50C．$\sqrt{2015}$-50D．50-$\sqrt{2015}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

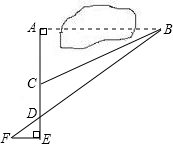    20．数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离，他们设计了如图所示的测量方案：从树A沿着垂直于AB的方向走到E，再从E沿着垂直于AE的方向走到F，C为AE上一点，其中3位同学分别测得三组数据：
    （1）AC，∠ACB；（2）EF、DE、AD；（3）CD，∠ACB，∠ADB，
    其中能根据所测数据求得A、B两树距离的有（1）（2）（3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

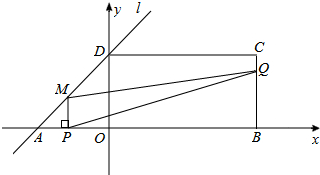    10．如图，在平面直角坐标系中，四边形ABCD是一个面积为48的直角梯形，∠C=90°，∠DAO=45°，AB∥CD，点B（10，0）直线l经过点A，D两点，且动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动，同时动点Q从点B出发以每秒4个单位的速度沿B→C→D的方向向点D运动，过点P作PM垂直于x轴，与折线A→D→C相交于点M，当P、Q两点中有一点到达终点时，另一点也随之停止运动，设点P，Q运动的时间为t秒（t＞0），△MPQ的面积为S．
    （1）点A的坐标为（-4，0）；直线l的解析式为y=x+4；
    （2）试求点Q与点M的相遇前S与t的函数关系式，并写出相应的t的取值范围；
    （3）随着P，Q两点的运动，当点M在线段DC上运动时，设PM的延长线与直线l相交于点N，试探究：当t为何值时，△QMN为等腰三角形，请直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．如图，将长为12cm，宽6cm的矩形纸片ABCD折叠，使点A与点C重合，则折痕EF的长为3$\sqrt{5}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

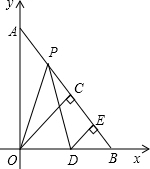    14．在△ABO中，∠AOB=90°，OA=OB=10，分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系，点P自点A出发沿线段AB匀速运动至点B停止．同时点D自原点O出发沿x轴正方向匀速运动．在点P、D运动的过程中，始终满足PO=PD，过点O、D向直线AB做垂线，垂足分别为点C、E，设OD=x．
    （1）求证：PC=BE；
    （2）在点P、D运动的过程中，线段PE的长是否是一个定值？若是定值，请求出这个定值；若不是定值，说明理由；
    （3）设以点P、O、D、E为顶点的四边形面积为y，请直接写出y与x的函数关系式，并写出自变量的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

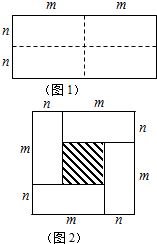    6．图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．
    （1）请写出图2中阴影部分的面积：（m-n）2或（m+n）2-4mn；
    （2）观察图2你能写出下列三个代数式之间的等量关系吗？代数式：（m+n）2，（m-n）2，mn．（m-n）2=（m+n）2-4mn；
    （3）根据（2）中的等量关系，解决如下问题：若a+b=7，ab=5，求a-b的值．

    查看答案和解析>>

    同步练习册答案