
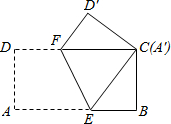
 如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm.
如图,将长为12cm,宽6cm的矩形纸片ABCD折叠,使点A与点C重合,则折痕EF的长为3$\sqrt{5}$cm. 分析 如图,首先证明四边形AECF为平行四边形;运用勾股定理分别求出CF、AC的长度,运用平行四边形的面积公式,即可解决问题.
解答 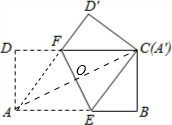 解:连接AC、AF;
解:连接AC、AF;
由题意得:EF⊥AC,且OA=OC;
∵四边形ABCD为矩形,
∴FC∥AE,∠OAE=∠OCF;
在△AOE与△COF中,
$\left\{\begin{array}{l}{∠AOE=∠COF}\\{AO=CO}\\{∠OAE=∠OCF}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴四边形AECF为平行四边形;
设AF=CF=λ,则DF=12-λ;由勾股定理得:
λ2=(12-λ)2+62,
解得:λ=7.5;
由勾股定理得:AC2=AB2+BC2,而AB=12,BC=6,
∴AC=6$\sqrt{5}$;
∵CF•AD=$\frac{1}{2}$AC•EF,
∴EF=3$\sqrt{5}$,
故答案为3$\sqrt{5}$.
点评 该题主要考查了翻折变换的性质、平行四边形的判定、勾股定理等几何知识点及其应用问题;牢固掌握翻折变换的性质等几何知识点是解题的基础和关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
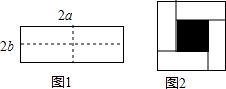 我们把如图1的一个长为2a,宽为2b的长方形,沿虚线剪成四个小长方形,再按如图2围成一个较大的正方形,则:
我们把如图1的一个长为2a,宽为2b的长方形,沿虚线剪成四个小长方形,再按如图2围成一个较大的正方形,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 68738×108 | B. | 687380×108 | C. | 6.8738×1013 | D. | 6.8738×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2 015 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com