
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
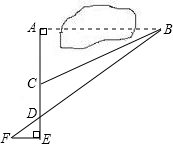 数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:
数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
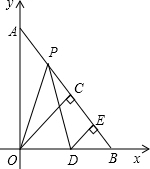 在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x.
在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O,求证:EF与BD互相平分.
如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O,求证:EF与BD互相平分.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
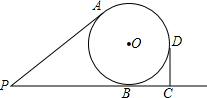 已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.
已知线段PA、PB分别与⊙O相切于点A、B,C为PB延长线上一点,CD⊥PC于C,线段CD与⊙O相切于点D,且PA=4,PC=6,则⊙O的半径R=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
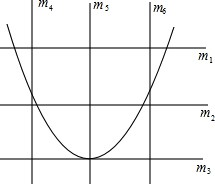 王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )
王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )| A. | m1,m4 | B. | m2,m3 | C. | m3,m6 | D. | m4,m5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com