
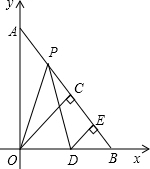
 在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x.
在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x.分析 (1)如图根据等腰三角形的性质和点P的位置讨论PC与PE的相等关系;(2)由(1)中的讨论可知PE的长为定值;(3)分0≤x<10,10≤x≤20两种情况,结合图形求得四边形PODE面积用x表示表达式.
解答 解:如图: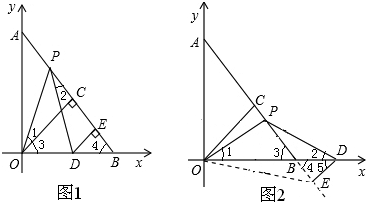
当0<x<10时,如图1,在RT△AOB中,AO=BO,故∠4=45°
∵OC⊥AB,∴$∠3=\frac{1}{2}∠AOB=45°$
∴∠3=∠4
∵PO=PD∴∠POD=∠PDO
即∠1+∠3=∠2+∠4
∴∠1=∠2
∵DE⊥AB,∴∠PCO=∠DEP=90°
∴△POC≌△DPE(AAS)…(2分)
∴PC=DE
而△DEB为等腰RT△,∴DE=BE
∴PC=BE…(1分)
当x=10时,PC=BE=0…(1分)
当10<x<20时,如图2,由上可知∠3=∠4=45°
且△DEB为等腰RT△,DE=BE,∠5=45°
∵PO=PD
∴∠1=∠2
∵∠CPO=∠1+∠3且∠PDE=∠2+∠5
∴∠CPO=∠PDE
且∠OCP=∠PED=90°
∴△POC≌△DPE(AAS)…(2分)
∴PC=DE=BE…(1分)
当x=0或20时,PC=BE=$5\sqrt{2}$…(1分)
(2)PE为定值,由(1)得当0≤x≤20时,PE=OC=$5\sqrt{2}$…(2分)
(3)当0<x<10时,如图,
①当0<x<10时
S四边形PODE=S△AOB-S△AOP-S△DEB
=$\frac{1}{2}×10×10-\frac{1}{2}×10×\frac{x}{2}-\frac{1}{2}(10-x)×\frac{1}{2}(10-x)$
=$-\frac{1}{4}{x}^{2}+\frac{5}{2}x+25$
∴$y=-\frac{1}{4}{x}^{2}+\frac{5}{2}x+25$;
②当10<x<20时,
${S}_{四边形PO{D}^{′}{E}^{′}=}{S}_{△PO{D}^{′}}+{S}_{△{D}^{′}O{E}^{′}}$
=$\frac{1}{2}x(10-\frac{x}{2})+\frac{1}{2}x•\frac{x-10}{2}$
=$\frac{5}{2}x$
∴$y=\frac{5}{2}x$…(2分)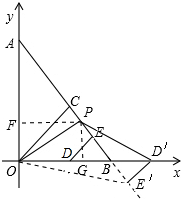
点评 本题是二次函数的综合题型,其中涉及到求几何图形面积通过几个三角形的面积求得.在求有关动点问题时要注意分析题意分情况讨论结果.


科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2 015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 △ABC与△DEC的位置关系如图所示,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=m,AB=n(n>m),则DF=$\frac{{n}^{2}-{m}^{2}}{m}$.
△ABC与△DEC的位置关系如图所示,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=m,AB=n(n>m),则DF=$\frac{{n}^{2}-{m}^{2}}{m}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
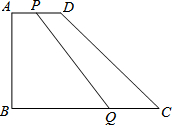 如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒,
如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动.当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com