
【题目】如图,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'CD',B'C与AD交于点E,AD的延长线与A′D′交于点F.
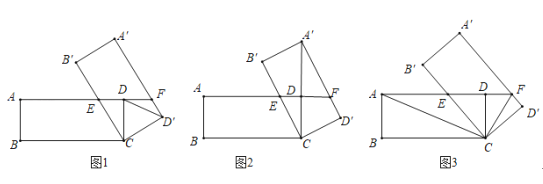
(1)如图1,当a=60°时,连接DD',求DD'和A'F的长;
(2)如图2,当矩形A′B′CD′的顶点A'落在CD的延长线上时,求EF的长;
(3)如图3,当AE=EF时,连接AC,CF,求证:∠ACF=90°.
【答案】(1)DD'=3;A'F= 4-![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)由旋转的性质可得CD=CD'=3,A'D'=AD=4,∠DCD'=60°,∠ADC=∠A'D'C=90°,由“HL”可证Rt△CDF≌Rt△CD'F,可得∠DCF=∠D'CF=30°,由锐角三角函数可求DF的长,即可求A'F的长;
(2)由勾股定理可求A'C=5,可得A'D=2,通过证明△ECD∽△A'CB',可得![]() ,可求DE的长,由平行线分线段成比例可得
,可求DE的长,由平行线分线段成比例可得![]() ,可求DF的长,即可求EF的长;
,可求DF的长,即可求EF的长;
(3)如图3,过点F作FG⊥B'C于G,由面积法可证EF=EC=AE,由直角三角形的判定可得∠ACF=90°.
(1)∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=4,
∵将矩形ABCD绕点C按顺时针方向旋转60°角,
∴CD=CD'=3,A'D'=AD=4,∠DCD'=60°,∠ADC=∠A'D'C=90°,
∴△DCD'是等边三角形,
∴DD'=CD=3,∠CDD'=∠CD'D=60°,
∴∠FDD'=∠FD'D=30°,
如图1,连接CF,
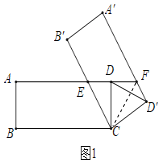
∵CD=CD',CF=CF,
∴Rt△CDF≌Rt△CD'F(HL)
∴∠DCF=∠D'CF=30°
∵tan∠DCF=![]() ,
,
∴DF=3×![]() ,
,
∴D'F=![]() ,
,
∴A'F=A'D'-D'F=4-![]() ,
,
(2)在Rt△A'B'C中,![]() ,
,
∵CD=3,
∴A'D=A'C-CD=2,
∵∠DCE=∠A'CB',∠CDE=∠B'=90°,
∴△ECD∽△A'CB',
∴![]()
∴![]()
∴DE=![]()
∵A'D'∥B'C
∴![]()
∴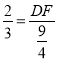
∴DF=![]()
∴EF=DE+DF=![]()
(3)如图3,过点F作FG⊥B'C于G,
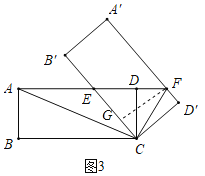
∴FG=CD'=3=CD,
∵S△CEF=![]() ×EF×CD=
×EF×CD=![]() ×EC×GF,
×EC×GF,
∴EF=EC
∵AE=EF,
∴AE=EF=EC,
∴△ACF是直角三角形,
∴∠ACF=90°


科目:初中数学 来源: 题型:
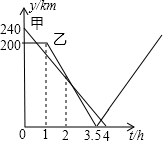
【题目】在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间.甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲、乙行驶过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.则当乙车到达A地时,甲车已在C地休息了_____小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
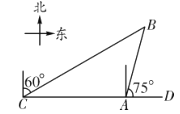
科目:初中数学 来源: 题型:
【题目】如图,港口![]() 在观测站
在观测站![]() 的正东方向
的正东方向![]() 处,某船从港口
处,某船从港口![]() 出发,沿东偏北
出发,沿东偏北![]() 方向匀速航行2小时后到达
方向匀速航行2小时后到达![]() 处,此时从观测站
处,此时从观测站![]() 处测得该船位于北偏东
处测得该船位于北偏东![]() 的方向,求该船航行的速度.
的方向,求该船航行的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
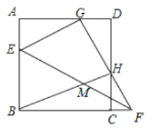
【题目】如图,正方形ABCD中,AB=6,E为AB边上一点,F是BC延长线上一点,将△BEF沿EF翻折,使点B恰好落在AD边上的点G处,FG与CD交于点H,连接BH,与EF交于点M,若BH平分∠CHG,AG=4,则EM=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中.

(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标;
三个顶点的坐标;
(2)直接写出△ABC的面积为 ;
(3)在x轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
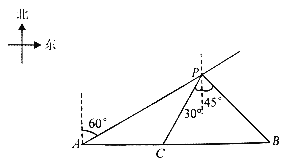
【题目】近日,国产航母山东舰成为了新晋网红,作为我国本世纪建造的第一艘真正意义上的国产航母,承载了我们太多期盼,促使我国在伟大复兴路上加速前行如图,山东舰在一次测试中,巡航到海岛A北偏东60°方向P处,发现在海岛A正东方向有一可疑船只B正沿BA方向行驶。山东舰经测量得出:可疑船只在P处南偏东45°方向,距P处![]() 海里。山东舰立即从P沿南偏西30°方向驶出,刚好在C处成功拦截可疑船只。求被拦截时,可疑船只距海岛A还有多少海里?(
海里。山东舰立即从P沿南偏西30°方向驶出,刚好在C处成功拦截可疑船只。求被拦截时,可疑船只距海岛A还有多少海里?(![]() ,结果精确到0.1海里)
,结果精确到0.1海里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
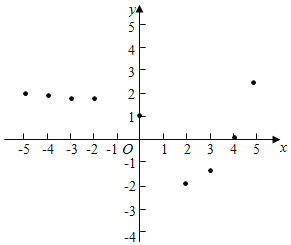
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小刚家,菜地,稻田在同一条直线上.小刚从家去菜地浇水,又去稻田除草,然后回家.如图反映了这个过程中,小刚离家的距离y与时间x之间的对应关系.如果菜地和稻田的距离为akm,小刚在稻田除草比在菜地浇水多用了bmin,则a,b的值分别为( )
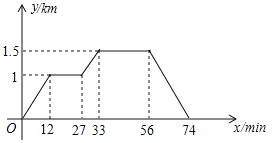
A.1,8B.0.5,12C.1,12D.0.5,8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com