
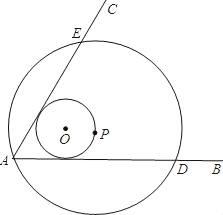
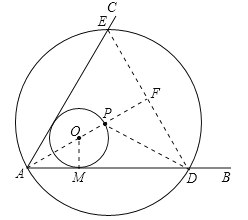
【题目】如图∠BAC=60°,半径长1的⊙O与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为( )
A. 3 B. 6 C. ![]() D.
D. ![]()
【答案】D
【解析】
连接AO并延长,与圆O交于P点,当AF垂直于ED时,线段DE长最大,设圆O与AB相切于点M,连接OM,PD,由对称性得到AF为角平分线,得到∠FAD为30度,根据切线的性质得到OM垂直于AD,在直角三角形AOM中,利用30度角所对的直角边等于斜边的一半求出AO的长,由AO+OP求出AP的长,即为圆P的半径,由三角形AED为等边三角形,得到DP为角平分线,在直角三角形PFD中,利用30度所对的直角边等于斜边的一半求出PF的长,再利用勾股定理求出FD的长,由DE=2FD求出DE的长,即为DE的最大值.
连接AO并延长,与ED交于F点,与圆O交于P点,此时线段ED最大,连接OM,PD,可得F为ED的中点.
∵∠BAC=60°,AE=AD,∴△AED为等边三角形,∴AF为角平分线,即∠FAD=30°.在Rt△AOM中,OM=1,∠OAM=30°,∴OA=2,∴PD=PA=AO+OP=3.在Rt△PDF中,∠FDP=30°,PD=3,∴PF=![]() ,根据勾股定理得:FD=
,根据勾股定理得:FD=![]() =
=![]() ,则DE=2FD=3
,则DE=2FD=3![]() .
.
故选D.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则sinB=![]() ,sinC=
,sinC=![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() ,同理有:
,同理有:![]() ,
,![]() ,所以
,所以![]() .
.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
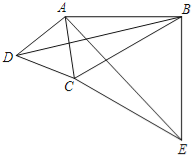
【题目】如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.
(1)求证:BD=AE;
(2)若AB=2,BC=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车早晨7∶00出发,从甲地驶往乙地送货.如图是货车行驶路程y(km)与行驶时间x(h)的完整的函数图像(其中点B、C、D在同一条直线上),小明研究图像得到了以下结论:
①甲乙两地之间的路程是100 km;
②前半个小时,货车的平均速度是40 km/h;
③8∶00时,货车已行驶的路程是60 km;
④最后40 km货车行驶的平均速度是100 km/h;
⑤货车到达乙地的时间是8∶24,
其中,正确的结论是( )

A.①②③④B.①③⑤C.①③④D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com