
分析 根据题意知an是-1、0、1、2中的某一个整数,从而可以分别设出含有-1、0、1、2的个数,然后根据题意,进行灵活变形,即可求得$a_1^3+a_2^3+…+a_{200}^3$的最大值与最小值.
解答 解:由题意可得,
an是-1、0、1、2中一个,
设整数a1,a2,…,a200中含有x个-1,y个1,z个2,则含有0的个数为200-x-y-z,
$\left\{\begin{array}{l}{x×(-1)+y×1+(200-x-y-z)×0+2z=200}\\{(-1)^{2}×x+{1}^{2}×y+{0}^{2}×(200-x-y-z)+{2}^{2}×z=300}\end{array}\right.$
化简,得
$\left\{\begin{array}{l}{-x+y+2z=200}\\{x+y+4z=300}\end{array}\right.$
解得-x+y=200-2z,$\left\{\begin{array}{l}{y-x=200-2z}\\{y+x=300-4z}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=50-z}\\{y=250-3z}\end{array}\right.$
∵$\left\{\begin{array}{l}{x+y+z≤200}\\{x+y≥0}\end{array}\right.$
∴$\left\{\begin{array}{l}{300-3z≤200}\\{300-4z≥0}\end{array}\right.$
解得$\frac{100}{3}≤z≤75$,
∴z的最小值为34,z的最大值为75,
∵$a_1^3+a_2^3+…+a_{200}^3$=(-1)3×x+13×y+23×z=-x+y+8z=200-2z+8z=200+6z,
∴当z=34时,200+6z取得最小值,200+6z=200+6×34=200+204=404,
当z=75时,200+6z取得最大值,200+6z=200+6×75=200+450=650,
即$a_1^3+a_2^3+…+a_{200}^3$的最大值是650,最小值是404.
点评 本题考查有理数的混合运算,解题的关键是明确题意,列出相应的关系式,找出所求问题需要的条件.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
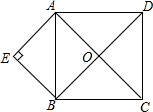 如图,点O为正方形ABCD的对角线的交点,E为正方形外一点,且AE⊥BE.
如图,点O为正方形ABCD的对角线的交点,E为正方形外一点,且AE⊥BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
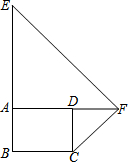 已知,E,F在矩形ABCD的边BA,AD延长线上.若EB=EF=8,CB=CF=6,求矩形ABCD的面积是$\frac{864}{25}$.
已知,E,F在矩形ABCD的边BA,AD延长线上.若EB=EF=8,CB=CF=6,求矩形ABCD的面积是$\frac{864}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com