
分析 如图作CH⊥BA于H,AM⊥BC于M,PN⊥BC于N,因为PN∥AM,得$\frac{PN}{AM}=\frac{PD}{AD}$,所以欲求AP需要求出AM、AD、PD,利用勾股定理以及RT△30度角的性质,求出CH、AH、再利用面积法求出AM、CM、BM,利用△BAD∽△BCA求出BD问题即可解决.
解答 解:如图作CH⊥BA于H,AM⊥BC于M,PN⊥BC于N,
∵∠BAC=120°,
∴∠CAH=180°-∠BAC=60°,
在RT△ACH中,∵AC=4,∠ACH=30°,
∴AH=2,HC=2$\sqrt{3}$,
在RT△BCH中,∵BH=4,HC=2$\sqrt{3}$,
∴BC=2$\sqrt{7}$,
∵$\frac{1}{2}$•BC•AM=$\frac{1}{2}$•AB•CH,
∴AM=$\frac{2\sqrt{21}}{7}$,
∵∠B=∠B,∠BAD=∠ACB,
∴△BAD∽△BCA,
∴$\frac{BA}{BC}=\frac{BD}{BA}$,
∴BD=$\frac{2\sqrt{7}}{7}$,
∵BM=$\sqrt{A{B}^{2}-A{M}^{2}}$=$\frac{4\sqrt{7}}{7}$,
∴DM=$\frac{2\sqrt{7}}{7}$,
∴AD=$\sqrt{D{M}^{2}+A{M}^{2}}$=$\frac{4\sqrt{7}}{7}$,
∵PN∥AM,
∴$\frac{PN}{AM}=\frac{PD}{AD}$,
∴$\frac{\frac{5\sqrt{21}}{7}}{\frac{2\sqrt{21}}{7}}=\frac{PD}{\frac{4\sqrt{7}}{7}}$,
∴PD=$\frac{10\sqrt{7}}{7}$,∴AP=2$\sqrt{7}$,
根据对称性DP′=$\frac{10\sqrt{7}}{7}$,AP=DP′-AD=$\frac{3\sqrt{7}}{7}$.
故答案为2$\sqrt{7}$或$\frac{3\sqrt{7}}{7}$.
点评 本题考查相似三角形的判定和性质、勾股定理、直角三角形30度角的性质等知识,解题的关键是利用120°构造特殊三角形(△ACH),学会应用面积法求高,属于中考常考题型.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A的坐标为(0,2),点p的坐标为(m,0)且m>0,一开口向上的抛物线以P为顶点,且经过点A.
如图,在平面直角坐标系中,点A的坐标为(0,2),点p的坐标为(m,0)且m>0,一开口向上的抛物线以P为顶点,且经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 序号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
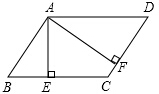 如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是80.
如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是80.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}-\sqrt{2}$ | B. | $\sqrt{2}-\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com