
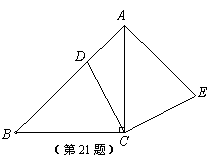
如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形.
 |
(1)解:∵∠ACB=90°∴∠BCD+∠ACD=90°∵∠DCE=90°∴∠ACD+∠ACE=90°
∴∠BCD=∠ACE………………………………………………………………………1分
在△CBD与△CAE中,∵CB=CA, ∠BCD=∠ACE,CD=CE,∴△CBD≌△CAE,
∴∠B=∠CAE, ………………………………………………………………………3分
∵∠B+∠BAC=90°∴∠BAC+∠EAC=90°∴AB⊥AE …………………………4分
(2)证:∵点D为AB中点,∴∠ADC=90°………………………………………6分
∵∠DCE=90°, ∠BAE=90°∴四边形ADCE是矩形,…………………………7分
∴CD=CE,∴四边形ADCE是正方形 ……………………………………………8分


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
2014年3月14日,“玉兔号”月球车成功在距地球约384 400公里远的月球上自主唤醒,将384 400精确到万位用科学记数法表示为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
有4-张正面分别标有数字-1、0、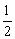 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为x,另有一个被均匀分成4份的转盘,上面分别标有数字-1、0、-4、-5,转动转盘,指针所指的数字记为y(若指针指在分割线上则重新转一次),请你用画树状图或列表格的方法求出点P(x,y)落在抛物线y=2x2-2x-4与x轴所围成的区域内(不含边界)的概率.
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为x,另有一个被均匀分成4份的转盘,上面分别标有数字-1、0、-4、-5,转动转盘,指针所指的数字记为y(若指针指在分割线上则重新转一次),请你用画树状图或列表格的方法求出点P(x,y)落在抛物线y=2x2-2x-4与x轴所围成的区域内(不含边界)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
某一次函数的函数关系为kx+(k+1)y=1(k是正整数),当k=1时,函数图像与两坐标轴所围成图形的面积为S1,当k=2时,面积为S2,…,当k=n时,面积为Sn,则S1+S2+…+Sn= .
查看答案和解析>>
科目:初中数学 来源: 题型:
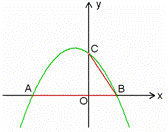
如图1,抛物线y=-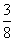 x2-
x2-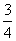 x+3与x轴交于
x+3与x轴交于
A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等
于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4, 0),M为直线l上的动点,当以A、B、M为
顶点所作的直角三角形有且只有三个时,求直线l的解析式.
|
|
|
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
学期初,学校体育组对九年级某班50名学生进行了跳远测试(满分5分),根据测试成绩制作了下面两个统计图(信息不完整)。
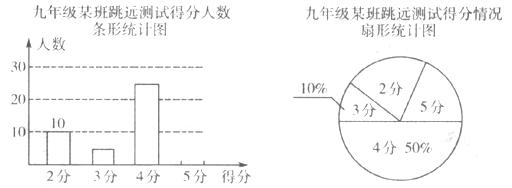
根据统计图解答下列问题:
(1)请补全条形统计图;
(2)本次测试的平均分是多少?
(3)通过一段时间的训练,体育组对该班50名学生进行第二次跳远测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中,得4分、5分的学生分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
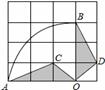
如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则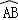 的长为( )
的长为( )
A.π B.6π C.3π D.1.5π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com