
【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数.
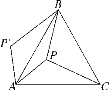
【答案】5,150°
【解析】
连接PP′,根据旋转的性质与等边三角形的判定可证得△AP′P为等边三角形,则PP′=AP=5,∠APP′=60°,在△BPP′中,利用勾股定理的逆定理易证△BPP′为直角三角形,∠BPP′=90°,然后计算求解即可.
解:如图,连接PP′,
∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,
∴△AP′P为等边三角形,
∴PP′=AP=5,∠APP′=60°,
在△BPP′中,
∵PP′=5,BP=12,BP′=13,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°,
即点P与点P′之间的距离为5,∠APB的度数为150°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
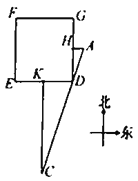
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为( )
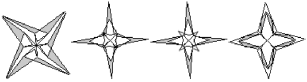
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
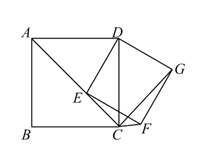
【题目】如图,已知四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG。
(1)求证:矩形DEFG是正方形。
(2)当点E从A点运动到C点时;
①求证:∠DCG的大小始终不变;
②若正方形ABCD的边长为2,则点G运动的路径长为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
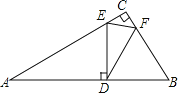
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+![]() 图象与x轴,y轴分别相交于A、B两点,与反比例函数y=
图象与x轴,y轴分别相交于A、B两点,与反比例函数y=![]() (k≠0)的图象相交于点E、F,过F作y轴的垂线,垂足为点C,已知点A(﹣3,0),点F(3,t).
(k≠0)的图象相交于点E、F,过F作y轴的垂线,垂足为点C,已知点A(﹣3,0),点F(3,t).
(1)求一次函数和反比例函数的表达式;
(2)求点E的坐标并求△EOF的面积;
(3)结合该图象写出满足不等式![]() ﹣ax≤
﹣ax≤![]() 的解集.
的解集.
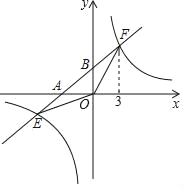
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com