【题目】如图，在△ABC中，∠B＝30°，∠C＝50°，AE是∠BAC的平分线，AD是高．
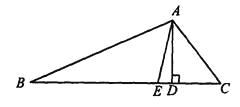
(1)求∠BAE的度数；
(2)求∠EAD的度数．
【答案】∠BAE为50°,∠EAD为10°。
【解析】
试题（1）根据△ABC的内角和定理求得∠BAC=100°；然后由角平分线的性质、△ABE的内角和定理来求∠BAE的度数；
（2）由三角形内角和定理可求得∠BAC的度数，在Rt△ADC中，可求得∠DAC的度数，AE是角平分线，有∠EAC=
∠BAC，故∠EAD=∠EAC-∠DAC．
解：（1）∵在△ABC中，∠B=30°，∠C=50°，
∴∠BAC=180°-∠B-∠C=100°；
又∵AE是∠BAC的平分线，
∴∠BAE=∠BAC=50°；
（2）∵AD是边BC上的高，
∴∠ADC=90°，
∴在△ADC中，∠C=50°，∠C+∠DAC=90°，
∴∠DAC=40°，
由（1）知，∠BAE=∠CAE=50°，
∴∠DAE=∠EAC-∠DAC=50°-40°=10°，即∠EAD=10°
科目：初中数学 来源： 题型：
【题目】用“※”定义一种新运算：对于任意有理数a和b，规定a※b＝ab2+2ab+a．
如：1※2＝1×22+2×1×2+1＝9
（1）（﹣2）※3＝ ；
（2）若
※3＝16，求a的值；
（3）若2※x＝m，（
x）※3＝n（其中x为有理数），试比较m，n的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】口袋中装有四个大小完全相同的小球，把它们分别标号1,2,3,4，从中随机摸出一个球，记下数字后放回，再从中随机摸出一个球，利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】
.
【解析】试题分析：
根据题意列表如下，由表可以得到所有的等可能结果，再求出所有结果中，两次所摸到小球的数字之和为4的次数，即可计算得到所求概率.
试题解析：
列表如下：
1 | 2 | 3 | 4 | |
1 | （1，1） | （1，2） | （1，3） | （1，4） |
2 | （2，1） | （2，2） | （2，3） | （2，4） |
3 | （3，1） | （3，2） | （3，3） | （3，4） |
4 | （4，1） | （4，2） | （4，3） | （4，4） |
由表可知，共有16种等可能事件，其中两次摸到的小球数字之和等于4的有（3，1）、（2，2）和（1，3），共计3种，
∴P（两次摸到小球的数字之和等于4）=
.
【题型】解答题
【结束】
23
【题目】小亮同学想利用影长测量学校旗杆AB的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上BD处，另一部分在某一建筑的墙上CD处，分别测得其长度为9.6米和2米，求旗杆AB的高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在△ABC中,∠ACB=90,BC=4,AC=3,线段PQ⊥BC于Q(如图,此时点Q与点B重合)，PQ=AB，当点P沿PB向B滑动时，点Q相应的从B沿BC向C滑动，始终保持PQ=AB不变，当△ABC与△PBQ全等时，PB的长度等于________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点M、N分别是正五边形ABCDE的边BC、CD上的点，且BM=CN，AM交BN于点P．
（1）求证：△ABM≌△BCN；
（2）求∠APN的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
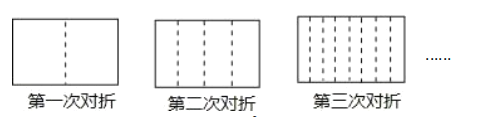
【题目】将一张长方形的纸对折，如图所示可得到一条折痕(图中虚线)．继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到
条折痕，那么对折四次可以得到（ ）条折痕．如果对折
次， 可以得到（ ）条折痕
A.
，
B.，
C.
，
D.
，
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,四边形ABCD中，∠B=90°, AB//CD，M为BC边上的一点，AM平分∠BAD，DM平分∠ADC，
求证:(1) AM⊥DM;
(2) M为BC的中点.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AC＞AB.
(1)作AB边的垂直平分线交BC于点P，作AC边的垂直平分线交BC于点Q，连接AP，AQ.(尺规作图，保留作图痕迹，不需要写作法)
(2)在(1)的条件下，若BC＝14，求△APQ的周长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点 A 是反比例函数 y 
在第一象限图象上的一个动点，连接 OA，以
OA 为长，OA为宽作矩形 AOCB，且点 C 在第四象限，随着点 A 的运动，点 C 也随之运动，但点 C 始终在反比例函数 y 
的图象上，则 k 的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com