
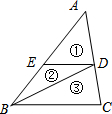
 如图,DE∥BC,连接BD,△ABC被分成①②③三部分,其中图形①和②的面积相等,则图形②和③的面积比为1:2.
如图,DE∥BC,连接BD,△ABC被分成①②③三部分,其中图形①和②的面积相等,则图形②和③的面积比为1:2. 分析 由“图形①和②的面积相等”得到点E是AB的中点,易推知ED是△ABC的中位线,则△AED∽△ABC,利用相似三角形的面积之比等于相似比的平方来求③的面积即可.
解答  解:如图,∵图形①和②的面积相等,图形①和②是同高的两个三角形,
解:如图,∵图形①和②的面积相等,图形①和②是同高的两个三角形,
∴AE=BE,即点E是AB的中点.
又∴ED是△ABC的中位线,且△AED∽△ABC,
∴$\frac{ED}{BC}$=$\frac{1}{2}$,
∴$\frac{{S}_{△AED}}{{S}_{△ABC}}$=($\frac{ED}{BC}$)2=$\frac{1}{4}$,
∴S△AED=$\frac{1}{4}$S△ABC,
∴$\frac{{S}_{△AED}}{{S}_{△BCD}}$=$\frac{1}{2}$,
∴$\frac{{S}_{△BED}}{{S}_{△BCD}}$=$\frac{1}{2}$,即图形②和③的面积比为 1:2.
故答案是:1:2.
点评 本题考查了三角形中位线定理,三角形的面积.此题利用了相似三角形的判定和相似三角形的面积之比等于相似比的平方来解题的.


科目:初中数学 来源: 题型:选择题
| A. | 通常温度降到0℃以下,纯净的水结冰 | |
| B. | 随意翻到一本书的某页,这页的页码是奇数 | |
| C. | 掷一枚普通正方体骰子,向上的一面是7点 | |
| D. | 测量某天的最低气温,结果为-150℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
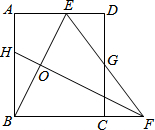 如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:| A. | ①③ | B. | ②③④ | C. | ①② | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
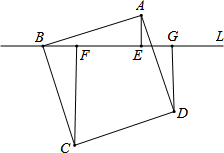 如图,过正方形ABCD的顶点B作直线L,过A,C,D作L的垂线.垂足分别为点E,F,G.若AE=2,CF=6,则CF+AE+DG的值为12.
如图,过正方形ABCD的顶点B作直线L,过A,C,D作L的垂线.垂足分别为点E,F,G.若AE=2,CF=6,则CF+AE+DG的值为12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
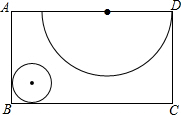 如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )
如图,矩形ABCD纸板中,剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若已知小圆的半径为1cm,则此圆锥的全面积是( )| A. | 2πcm | B. | 3πcm | C. | $\sqrt{3}$πcm | D. | ($\sqrt{3}$+1)πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
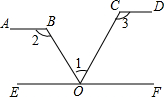 如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
如图,如果AB∥EF,EF∥CD,下列各式正确的是( )| A. | ∠1+∠2-∠3=90° | B. | ∠1-∠2+∠3=90° | C. | ∠1+∠2+∠3=90° | D. | ∠2+∠3-∠1=180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com