练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图，在四边形ABCD中，∠A=90°，AD=8．对角线BD⊥CD，P是BC边上一动点，连结PD．若∠ADB=∠C，则PD长的最小值为8．

    分析 根据垂线段最短，当DP垂直于BC的时候，DP的长度最小．结合已知条件，利用三角形的内角和定理推出∠ABD=∠CBD，由角平分线性质即可得AD=DP，由AD的长可得DP的长．

    解答 解：根据垂线段最短，当DP⊥BC的时候，DP的长度最小．
    ∵BD⊥CD，即∠BDC=90°，又∠A=90°，
    ∴∠A=∠BDC，又∠ADB=∠C，
    ∴∠ABD=∠CBD，又DA⊥BA，BD⊥DC，
    ∴AD=DP，又AD=8，
    ∴DP=8．
    故答案为：8．

    点评 本题考查了角平分线上的点到角的两边距离相等的性质，垂线段最短的性质，熟记性质并判断出DP最小时的位置是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

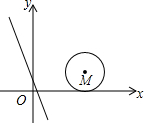    17．如图，在平面直角坐标系中，半径为2的⊙M的圆心坐标是（4，2），将直线y=-2x+1向上平移k个单位后恰好与⊙M相切，则k的值是（　　）
    A．1+$\sqrt{5}$或1+2$\sqrt{5}$B．1+2$\sqrt{5}$或1+4$\sqrt{5}$C．9+2$\sqrt{5}$或9-2$\sqrt{5}$D．10+2$\sqrt{5}$或10-2$\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图所示，若a∥b，∠1=120°，则∠2=（　　）
    A．55°B．60°C．65°D．75°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，已知AB∥CD，CE平分∠ACD，当∠A=120°时，∠ECD的度数是30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．如图是由6个完全相同的小正方体组成的几何体，其左视图为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

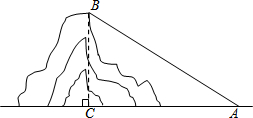    12．如图，在莲花山滑雪场滑雪，需从山脚下乘缆车上山，缆车索道与水平线所成的角为32°，缆车速度为每分钟50米，从山脚下A到达山顶B缆车需要16分钟，求山的高度BC．（精确到0.1米）
    [参考数据：sin32°=0.5299，cos32°=0.8480，tan32°=0.6249]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：$\sqrt{8}-4sin45°-{2^{-1}}+（2013-π{）^0}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

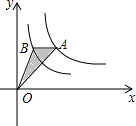    16．如图，点A和点B在第一象限，A是双曲线y=$\frac{3}{x}$上的一点，B是双曲线y=$\frac{1}{x}$上的一点，且AB平行于x轴，连接OA，OB，则△AOB的面积为1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，∠CAD和∠CBD都是直角，M是CD的中点，N是AB的中点．求证：直线MN是AB的垂直平分线．

    查看答案和解析>>

    同步练习册答案