
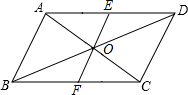
 如图,在?ABCD中,AC,BD交于点O,E是AD的中点,EO的延长线交BC于点F.求证:
如图,在?ABCD中,AC,BD交于点O,E是AD的中点,EO的延长线交BC于点F.求证:
|
| 1 |
| 2 |


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
| A、1.5×104美元 |
| B、1.5×105美元 |
| C、1.5×1012 美元 |
| D、1.5×1013美元 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
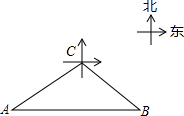 已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50,
已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50,| 2 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
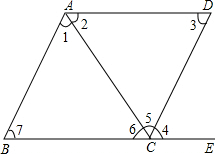 如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.
如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
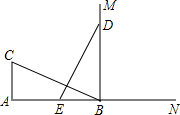 如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过
如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com