
【题目】在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
(1)旋转过程中,当MN和AC平行时,求正方形OABC旋转的角度;
(2)试证明旋转过程中,△MNO的边MN上的高为定值;
(3)折△MBN的周长为p,在旋转过程中,p值是否发生变化?若发生变化,说明理由;若不发生变化,请给予证明,并求出p的值.
【答案】
(1)
解:如图1中,
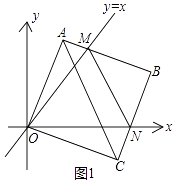
∵四边形OABC是正方形,
∴∠BAC=∠BCA=45°,BA=BC,OA=OC,∠OAB=∠OCB=90°
∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°,
∴∠BMN=∠BNM.
∴BM=BN,
∴AM=CN.
在△OAM与△OCN中,
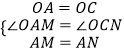
∴△OAM≌△OCN(SAS),
∴∠AOM=∠CON,
∴∠AOM=∠CON=22.50,
∴MN∥AC时,旋转角为22.50.
(2)
解:证明:如图2中,
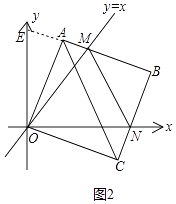
过点O作OF⊥MN于F,延长BA交y轴与E点,则∠AOE=45°﹣∠AOM,∠CON=45°﹣∠AOM.
∴∠AOE=∠CON.
在△OAE与△OCN中,
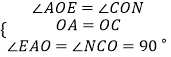
∴△OAE≌△OCN(ASA),
∴OE=ON,AE=CN.
在△OME与△OMN中,
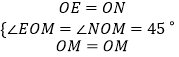
∴△OME≌△OMN(SAS),
∴∠OME=∠OMN.
∵MA⊥OA,MF⊥OF.
∴OA=OF=2,
∴在旋转过程中,高为定值.
(3)
解:旋转过程中,p值不变化.
理由:∵△OME≌△OMN,
∴ME=MN,
∵AE=CN,
∴MN=ME﹣AM+AE=AM+CN.
∴p=MN+BN+BM=AM+CN+BN+BM=AB+AC=4.
∴△MBN的周长p为定值.
【解析】(1)只要证明△AOM≌△CON,推出∠AOM=∠CON=22.5°即可解决问题.(2)如图2中,过点O作OF⊥MN于F,延长BA交y轴与E点,则∠AOE=45°﹣∠AOM,∠CON=45°﹣∠AOM.先证明△OAE≌△OCN(ASA),再证明△OME≌△OMN(SAS),推出∠OME=∠OMN,利用角平分线性质定理即可解决问题.(3)由(2)可知,MN=AM+CN,可以推出△BMN的周长为BA+BC是定值.
【考点精析】本题主要考查了图形的旋转的相关知识点,需要掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=![]() .例如18=1×18=2×9=3×6,这时就有F(18)=
.例如18=1×18=2×9=3×6,这时就有F(18)=![]() .请解答下列问题:
.请解答下列问题:
(1)计算:F(24);
(2)当n为正整数时,求证:F(n3+2n2+n)=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的费用;
(2)若有50名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
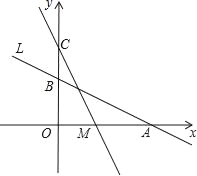
【题目】如图,直线L:y=-![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第10(n是大于0的整数)个图形需要黑色棋子的个数是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
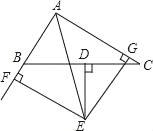
【题目】如图,在△ABC中,BC边上的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC于点G.
求证:(1)BF=CG;
(2)AB+AC=2AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并在括号内加注理由。
如图,已知![]() ∥
∥![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]()

求证:![]()
证明:∵![]() ∥
∥![]()
∴![]() = ( )
= ( )
∵![]() 、
、![]() 平分
平分![]() 、
、![]()
∴![]() =
=![]()
∴![]() =
=![]() ( )
( )
∴![]() =
=![]()
∴ ∥ ( )
∴![]() =∠ ( )
=∠ ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com