【题目】如图，折叠长方形一边AD，点D落在BC边的点F处，BC=10cm，AB=8cm。
求：（1）FC的长；
（2）EF的长。
【答案】（1）FC= 4cm；（2）EF=5cm.
【解析】试题分析：（1）根据折叠的性质可得AD=AF=10cm，在Rt△ABF中利用勾股定理计算出BF的长，进而得到FC的长；（2）由题意可得EF=DE，设DE=EF=xcm，则EC=（8-x）cm，在Rt△EFC中利用勾股定理可得（8-x）2+42=x2，再解方程即可得答案．
试题解析：
（1）由题意可得，AF=AD=10cm，在Rt△ABF中，∵AB=8，
∴BF=6cm，
∴FC=BC﹣BF=10﹣6=4cm；
（2）由题意可得EF=DE，可设DE的长为x，则在Rt△EFC中，(8﹣x)2+42=x2，解得x=5，即EF的长为5cm.
出彩同步大试卷系列答案科目：初中数学 来源： 题型：
【题目】已知：有理数m所表示的点到点2距离3个单位，a、b互为相反数，且都不为零，c、d互为倒数．
（1）求m的值；
（2）求代数式：2（a+b）+（
﹣3cd）﹣m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
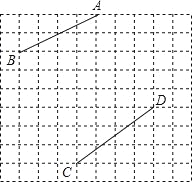
【题目】如图，在每个小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A、B、C、D均在小正方形的顶点上．
（1）在方格纸中画以AB为斜边的等腰直角三角形ABE；
（2）在方格纸中画以CD为一边的三角形CDF，点F在小正方形的顶点上，且三角形CDF的面积为5，tan∠DCF=
，连接EF，并直接写出线段EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在四边形ABCD中，AD∥BC，分别添加下列条件：①AB∥CD；②AB＝CD；③AD＝BC；④∠B＝∠D；⑤∠A＝∠C，其中能使四边形ABCD成为平行四边形的条件有( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
