
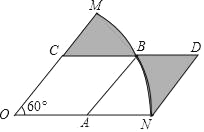
【题目】如图,在扇形MON中,圆心角∠MON=60°,边长为2的菱形OABC的顶点A,C,B分别在ON,OM和![]() 上,且ND∥AB,交CB的延长线于点D,则阴影部分的面积是_____.
上,且ND∥AB,交CB的延长线于点D,则阴影部分的面积是_____.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G.点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E.连接AD、DE,若CF=2,AF=3.给出下列结论:
,连接AF并延长交⊙O于点E.连接AD、DE,若CF=2,AF=3.给出下列结论:
①△ADF∽△AED;②FG=2;③tan∠E=![]() ;④S△DEF=4
;④S△DEF=4![]() .
.
其中正确的是( )
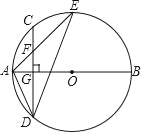
A. ①②④ B. ①②③ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
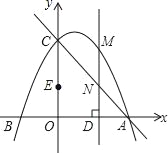
【题目】如图,抛物线y=﹣![]() +bx+c经过A(4,0),C(0,4)两点,点B是抛物线与x轴的另一个交点,点E是OC的中点,作直线AC、点M在抛物线上,过点M作MD⊥x轴,垂足为点D,交直线AC于点N,设点M的横坐标为m,MN的长度为d.
+bx+c经过A(4,0),C(0,4)两点,点B是抛物线与x轴的另一个交点,点E是OC的中点,作直线AC、点M在抛物线上,过点M作MD⊥x轴,垂足为点D,交直线AC于点N,设点M的横坐标为m,MN的长度为d.
(1)直接写出直线AC的函数关系式;
(2)求抛物线对应的函数关系式;
(3)求d关于m的函数关系式;
(4)当以点M、N、E、O为顶点的四边形为平行四边形时,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长为12cm,宽为5cm,高为8cm的长方体,一只蜘蛛从一条侧棱的中点A沿着长方体表面爬行到顶点B去捕捉蚂蚁,此时蜘蛛爬行的最短距离是( )
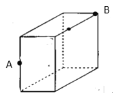
A.13 cmB.15 cmC.21 cmD.25cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形ABCD中,AB=CD=5 cm, BC=12 cm,点P从点B出发,以2cm/s的速度沿BC向点C运动,设点P的运动时间为ts.
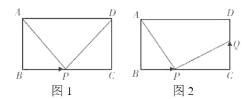
(1)PC=___cm;(用含t的式子表示)
(2)当t为何值时,△ABP≌△DCP?.
(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻△ABP与以P,Q,C为顶点的直角三角形全等?若存在,请求出v的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,对![]() 进行循环往复的轴对称变换,若原来点
进行循环往复的轴对称变换,若原来点![]() 坐标是
坐标是![]() ,则第1次变换后
,则第1次变换后![]() 点的坐标是__________,经过第284次变换后所得的
点的坐标是__________,经过第284次变换后所得的![]() 点坐标是__________.
点坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折得到△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )

A. 115° B. 105° C. 95° D. 85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com