
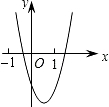
 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=-bx+b2-4ac与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系内的图象大致为( )
二次函数y=ax2+bx+c的图象如图所示,则一次函数y=-bx+b2-4ac与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系内的图象大致为( )| A. |  | B. | 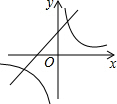 | C. |  | D. |  |
分析 根据二次函数图象确定-b、b2-4ac、a-b+c的符号,由它的符号判定一次函数图象与反比例函数图象所经过的象限即可.
解答  解:如图,抛物线y=ax2+bx+c的开口方向向上,则a>0.
解:如图,抛物线y=ax2+bx+c的开口方向向上,则a>0.
对称轴在y轴的右侧,则a、b异号,所以b<0,故-b>0.
又因为抛物线与x轴有2个交点,
所以b2-4ac>0,
所以直线y=-bx+b2-4ac经过第一、二、三象限.
当x=-1时,y>0,即a-b+c>0,所以双曲线y=$\frac{a-b+c}{x}$经过第一、三象限.
综上所述,符合条件的图象是B选项.
故选:B.
点评 本题综合考查了一次函数、二次函数以及反比例函数的图象.熟练掌握图象与函数关系式中系数的关系是解题的关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:选择题
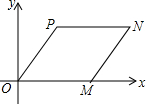 如图所示,在平面直角坐标系中,菱形OMNP的顶点P的坐标为(3,4),则顶点N的坐标是( )
如图所示,在平面直角坐标系中,菱形OMNP的顶点P的坐标为(3,4),则顶点N的坐标是( )| A. | (7,4) | B. | (8,4) | C. | (9,4) | D. | (10,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
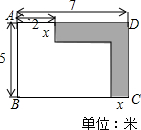 如图所示,客厅的地面是矩形ABCD,在它的一角摆放宽度相等的一张“7”字形的沙发,供会客用,要求摆放沙发后客厅地面的剩余面积为26平方米.若设沙发的宽度为x米,求x的值.
如图所示,客厅的地面是矩形ABCD,在它的一角摆放宽度相等的一张“7”字形的沙发,供会客用,要求摆放沙发后客厅地面的剩余面积为26平方米.若设沙发的宽度为x米,求x的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.2p2q与0.2pq2 | B. | $\frac{1}{3}{x}^{2}y$与-3xy2 | C. | m2n3与-m2n3 | D. | 0与-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
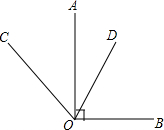 已知,如图,OA⊥BO于点O,OC是∠AOB外部一条射线,且∠AOC=40°,又OD平分∠COB,求∠AOD的度数.
已知,如图,OA⊥BO于点O,OC是∠AOB外部一条射线,且∠AOC=40°,又OD平分∠COB,求∠AOD的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com