
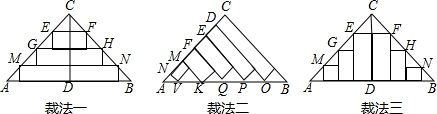
分析 利用相似三角形的性质,等腰直角三角形的性质分别求出总长度即可比较.
解答 解:∵AC=BC=40,∠ACB=90°,
∴AB=40$\sqrt{2}$,
∵CD⊥AB,
∴CD=$\frac{AC•BC}{AB}=20\sqrt{2}$,
裁发一中:
每张纸条宽度均为5$\sqrt{2}$,
第一张纸条长度记作a,则$\frac{20\sqrt{2}-5\sqrt{2}}{20\sqrt{2}}=\frac{a}{40\sqrt{2}}$,解得:a=30$\sqrt{2}$;
第二张纸条宽度记作b,则$\frac{20\sqrt{2}-2×5\sqrt{2}}{20\sqrt{2}}=\frac{b}{40\sqrt{2}}$,解得:b=20$\sqrt{2}$;
第三张纸条宽度记作c,则$\frac{20\sqrt{2}-3×5\sqrt{2}}{20\sqrt{3}}=\frac{c}{40\sqrt{2}}$,解得:c=10$\sqrt{2}$;
故第一种裁法中纸条总长度为:60$\sqrt{2}$;
裁法二中:纸条长度分别为40-5$\sqrt{2}$,40-2×$5\sqrt{2}$,40-3×$\sqrt{2}$,40-4×$5\sqrt{2}$,40-5×$5\sqrt{2}$,
故总长度为200-75$\sqrt{2}$;
裁法三中,纸条长度有2个(20$\sqrt{2}$-5$\sqrt{2}$),2个(20$\sqrt{2}$-2×$5\sqrt{2}$),2个(20$\sqrt{2}$-3×$5\sqrt{2}$),
故总长度为60$\sqrt{2}$;
∵200-75$\sqrt{2}$>60$\sqrt{2}$.
故裁法二中的纸条最长.
点评 本题考查相似三角形的性质、等腰直角三角形的性质、勾股定理等知识,利用等腰直角三角形的性质是解决问题的关键.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:填空题
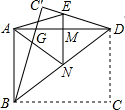 如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于M,则ME=$\frac{7}{12}$.
如图,一张宽为3,长为4的矩形纸片ABCD,先沿对角线BD对折,点C落在C′的位置,BC′交AD于G,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于M,则ME=$\frac{7}{12}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
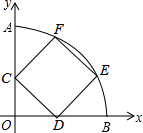 如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )
如图,以坐标原点O为圆心的圆弧交y轴于点A(0,5),交x轴于点B,正方形CDEF内接于扇形AOB(其中C在y轴上、D在x轴上,E、F在$\widehat{AB}$上),则正方形CDEF的边长为( )| A. | 3 | B. | $\frac{5(\sqrt{5}-1)}{2}$ | C. | $\sqrt{10}$ | D. | 以上都不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
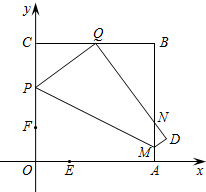 如图,四边形OABC为正方形,点A在x轴上,点C在y轴上,点B(8,8),点P在边OC上,点M在边AB上.把四边形OAMP沿PM对折,PM为折痕,使点O落在BC边上的点Q处.动点E从点O出发,沿OA边以每秒1个单位长度的速度向终点A运动,运动时间为t,同时动点F从点O出发,沿OC边以相同的速度向终点C运动,当点E到达点A时,E、F同时停止运动.
如图,四边形OABC为正方形,点A在x轴上,点C在y轴上,点B(8,8),点P在边OC上,点M在边AB上.把四边形OAMP沿PM对折,PM为折痕,使点O落在BC边上的点Q处.动点E从点O出发,沿OA边以每秒1个单位长度的速度向终点A运动,运动时间为t,同时动点F从点O出发,沿OC边以相同的速度向终点C运动,当点E到达点A时,E、F同时停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 菱形的周长等于两条对角线长之和的两倍 | |
| C. | 对角线相等的平行四边形是菱形 | |
| D. | 菱形的面积等于两条对角线长之积的一半 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com