
【题目】附加题:在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,
,
(1)求抛物线的对称轴;
(2)求点![]() 坐标(用含
坐标(用含![]() 的式子表示);
的式子表示);
(3)已知点![]() ,
,![]() ,若抛物线与线段
,若抛物线与线段![]() 恰有一个公共点,结合函数图像,求
恰有一个公共点,结合函数图像,求![]() 的取值范围.
的取值范围.
【答案】(1)直线x=0;(2)B(0,![]() );(3)
);(3)![]() ≤a≤
≤a≤![]() 或
或![]() ≤a≤
≤a≤![]()
【解析】
(1)根据抛物线的表达式直接得出对称轴即可;
(2)根据题意得出点A的坐标,再利用关于x轴对称的点的坐标规律得出点B坐标;
(3)分a>0和a<0两种情况分别讨论,画图图像,求出a的范围.
解:(1)在抛物线![]() 中,
中,
![]() ,
,
∴对称轴为直线x=0,即y轴;
(2)∵抛物线与![]() 轴交于点
轴交于点![]() ,
,
∴A(0,![]() ),
),
∵点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,
,
∴B(0,![]() );
);
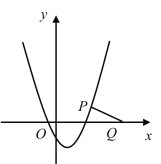
(3)当a>0时,点A(0,![]() )在y轴负半轴上,
)在y轴负半轴上,
当点P恰好在抛物线上时,代入得:![]() ,
,
解得:![]() 或
或![]() (舍),
(舍),
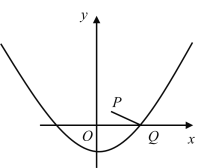
当点Q恰好在抛物线上时,代入得:![]() ,
,
解得:![]() 或
或![]() (舍),
(舍),
∴当![]() ≤a≤
≤a≤![]() 时,抛物线与线段PQ恰有一个公共点;
时,抛物线与线段PQ恰有一个公共点;
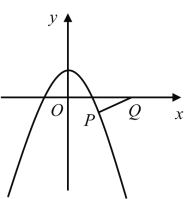
当a<0时,点A(0,![]() )在y轴正半轴上,
)在y轴正半轴上,
同理可知:
当点P恰好在抛物线上时,代入得:![]() ,
,
解得:![]() (舍)或
(舍)或![]() ,
,
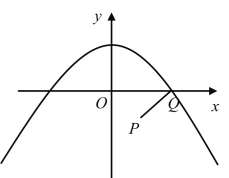
当点Q恰好在抛物线上时,代入得:![]() ,
,
解得:![]() (舍)或
(舍)或![]() ,
,
∴当![]() ≤a≤
≤a≤![]() 时,抛物线与线段PQ只有一个公共点;
时,抛物线与线段PQ只有一个公共点;
综上:若抛物线与线段![]() 恰有一个公共点,a的取值范围是
恰有一个公共点,a的取值范围是![]() ≤a≤
≤a≤![]() 或
或![]() ≤a≤
≤a≤![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
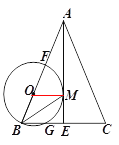
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌、B舞蹈、C朗诵、D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:

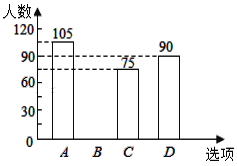
请结合统计图表,回答下列问题:
(1)本次调查的学生共____人,a=______, 并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对于随机事件的概率的描述:
①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;
②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2;
③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85
其中合理的有______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2.
(1)请用含有b的代数式表示c: ;
(2)若点B在直线l上,且B的横坐标为-1,点C的坐标为(b,5).
①若抛物线M还过点B,直接写出该抛物线的解析式;
②若抛物线M与线段BC恰有一个交点,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②.则三视图发生改变的是( )

A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com