
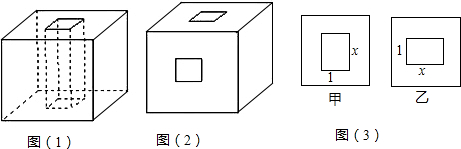
分析 (1)打孔后的表面积=原正方体的表面积-小正方形孔的面积+孔中的四个矩形的面积.
(2)打孔后的表面积=图(1)的表面积-4个小正方形孔的面积+新打的孔中的八个小矩形的面积
(3)分两种情形分别列出方程求解即可.
解答 解:(1)表面积S1=96-2+4×4=110(cm2);
故答案为110.
(2)表面积S2=S1-4+4×1.5×2=118(cm2);
故答案为118.
(3)能使橡皮泥块的表面积为130cm2,理由为:
①如图甲通孔,由题意,96-2-2(4-x)+3(2+2x)=130,
方程无解,不合题意.
②如图乙通孔,由题意,96-2-2x+4×3+4(2+2x)-2=130,
解得x=3,
∴当边长改为3cm时,表面积为130cm2.
点评 此题考查一元一次方程的实际运用,掌握长方体的表面积计算公式是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | x为任意实数 | B. | 3≤x≤5 | C. | x≤3 | D. | x≥5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
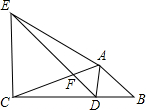 如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时.
如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.
在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com