
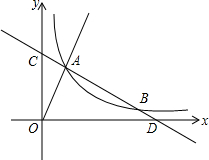
 已知直线y=$\frac{1}{2}$x+$\frac{5}{2}$与反比例函数y=$\frac{m}{x}$图象相交于点A、B,OA⊥AB.
已知直线y=$\frac{1}{2}$x+$\frac{5}{2}$与反比例函数y=$\frac{m}{x}$图象相交于点A、B,OA⊥AB. 分析 (1)根据直线的解析式求得D、C的交点坐标,从而求得OD、OC、CD的出,然后通过证得△AOC∽△DOC,即可求得OA的长.
(2)作AE⊥x轴,先证得△OAC∽△AEO,求得AE,进而根据勾股定理求得OE,得出A的坐标,代入反比例函数的解析式即可求得m的值.
(3)设B(a,b),由A(1,2),D(5,0)可知1<a<5,0<b<2,因为a为整数,所以a的取值为2、3、4,根据ab=m=2即可求得b的值,把三组值分别代入直线的解析式即可判定B的坐标.
解答 解:(1)由直线y=-$\frac{1}{2}$x+$\frac{5}{2}$可知:D(5,0),C(0,$\frac{5}{2}$),
∴OD=5,OC=$\frac{5}{2}$,
∴CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=$\frac{5\sqrt{5}}{2}$,
∵OA⊥AB,
∴∠OAC=∠DOC=90°,
∵∠ACO=∠OCD,
∴△AOC∽△DOC,
∴$\frac{OA}{OD}$=$\frac{OC}{CD}$,即$\frac{OA}{5}$=$\frac{\frac{5}{2}}{\frac{5\sqrt{5}}{2}}$,
∴OA=$\sqrt{5}$.
故答案为$\sqrt{5}$.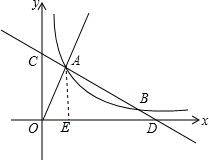 (2)作AE⊥x轴,
(2)作AE⊥x轴,
∴AE∥OC,
∴∠AOC=∠OAE,
∵∠OAC=∠AEO=90°,
∴△OAC∽△AEO,
∴$\frac{AE}{OA}$=$\frac{OA}{OC}$,即$\frac{AE}{\sqrt{5}}$=$\frac{\sqrt{5}}{\frac{5}{2}}$,
∴AE=2,
∴OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=1,
∴A(1,2),
∴m=1×2=2.
(3)∵A(1,2),D(5,0),
设B(m,n),则1<m<5,0<n<2,
∴B的坐标可能是(2,1),(3,$\frac{2}{3}$),(4,$\frac{1}{2}$),
代入y=-$\frac{1}{2}$x+$\frac{5}{2}$可知,B为(4,$\frac{1}{2}$)适合;
∴B的坐标为(4,$\frac{1}{2}$).
点评 此题主要考查了反比例函数和一次函数的交点问题以及函数图象上点的坐标特征,关键是利三角形相似计算出A点坐标.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
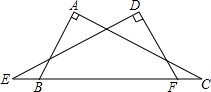 如图所示,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF,∠ABC=70°,AC=4.求∠E的度数和DE的长.
如图所示,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF,∠ABC=70°,AC=4.求∠E的度数和DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
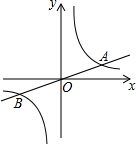 如图所示:已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A,B两点,且点A的横坐标为4
如图所示:已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$交于A,B两点,且点A的横坐标为4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
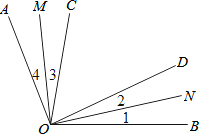 如图,已知∠AOB=120°,∠COD=50°,OM平分∠BOD,即∠1=∠2,ON平分∠AOC,即∠3=∠4;
如图,已知∠AOB=120°,∠COD=50°,OM平分∠BOD,即∠1=∠2,ON平分∠AOC,即∠3=∠4;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
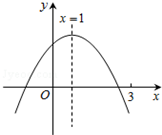 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有②③⑤.
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有②③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
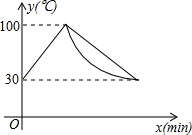 饮水机接通电源就进入自动程序,若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图.开机加热时每分钟上升10℃,加热到100℃,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至30℃,饮水机自动开机,重复上述自动程序.若上午7:20开机,则8:00时能否喝到超过50℃的水?说明理由.
饮水机接通电源就进入自动程序,若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图.开机加热时每分钟上升10℃,加热到100℃,饮水机关机停止加热,水温开始下降,下降时水温与开机后的时间成反比例关系.当水温降至30℃,饮水机自动开机,重复上述自动程序.若上午7:20开机,则8:00时能否喝到超过50℃的水?说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com