
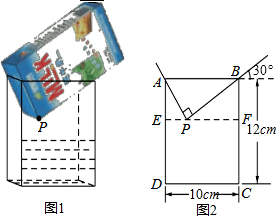
 将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入,图2是它的平面示意图,请根据图中的信息解答下列问题:
将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入,图2是它的平面示意图,请根据图中的信息解答下列问题:分析 (1)解Rt△ABP,根据含30°角的直角三角形的性质得出AP=$\frac{1}{2}$AB=5cm,BP=$\sqrt{3}$AP=$5\sqrt{3}$cm;
(2)先由EF∥AB,得出∠BPF=∠ABP=30°,再解Rt△BFP,得出BF=$\frac{1}{2}$BP=$\frac{{5\sqrt{3}}}{2}$cm,那么CF=BC-BF≈7.7cm.
解答 解:(1)在Rt△ABP中,∵∠APB=90°,∠ABP=30°,AB=10cm,
∴AP=$\frac{1}{2}$AB=5cm,BP=$\sqrt{3}$AP=$5\sqrt{3}$cm;
(2)∵EF∥AB,
∴∠BPF=∠ABP=30°,
又∵∠BFP=90°,
∴BF=$\frac{1}{2}$BP=$\frac{{5\sqrt{3}}}{2}$cm,
∴CF=BC-BF=12-$\frac{{5\sqrt{3}}}{2}$≈7.7(cm).
即容器中牛奶的高度CF约为7.7cm.
故答案为5,5$\sqrt{3}$.
点评 此题主要考查了解直角三角形的应用,掌握含30°角的直角三角形的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2+bx+c的图象经过点(0,-3),(1,0).
已知二次函数y=x2+bx+c的图象经过点(0,-3),(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
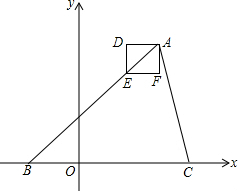 如图,在平面直角坐标系中,△ABC的边BC在x轴上,点A、B的坐标分别为(3,4)(-2,0),边长为$\frac{9}{8}$的正方形ADEF的位置如图所示,且边AD与x轴平行.将正方形ADEF沿平行于y轴方向向下平移$\frac{5}{2}$个单位长度,再沿平行于x轴方向向左平移m(m>0)个单位长度,如果平移后的正方形的顶点E在△ABC的内部,则m的取值范围是0<m<3.40625.
如图,在平面直角坐标系中,△ABC的边BC在x轴上,点A、B的坐标分别为(3,4)(-2,0),边长为$\frac{9}{8}$的正方形ADEF的位置如图所示,且边AD与x轴平行.将正方形ADEF沿平行于y轴方向向下平移$\frac{5}{2}$个单位长度,再沿平行于x轴方向向左平移m(m>0)个单位长度,如果平移后的正方形的顶点E在△ABC的内部,则m的取值范围是0<m<3.40625.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com