
【题目】某同学进行社会调查,随机抽查了某小区的40户家庭的年收入(万元)情况,并绘制了如图不完整的频数直方图,每组包括前一个边界值,不包括后一个边界值.
(1)补全频数直方图.
(2)年收入的中位数落在哪一个收入段内?
(3)如果每一组年收入均以最低计算,这40户家庭的年平均收入至少为多少万元?
(4)如果该小区有1200户住户,请你估计该小区有多少家庭的年收入低于18万元?
【答案】
(1)解:由题意可得,
26≤x<30的用户有:40﹣4﹣4﹣6﹣12﹣4=10
补全的频数直方图如右下所示,
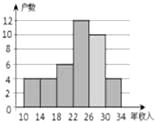
(2)解:由条形统计图可得,
中位数落在22万元至26万元收入段内
(3)解:由题意可得,
这40户家庭的年平均收入至少为:
![]()
=21.2(万元),
即这40户家庭的年平均收入至少为21.2万元
(4)解:由题意可得,
1200× ![]() (户)
(户)
即该小区有240户家庭的年收入低于18万元
【解析】(1)26≤x<30的用户=用某小区的40户家庭-10≤x<14的用户-14≤x<18的用户-18≤x<22的用户-30≤x<34的用户-26≤x<30的用户,根据数据补全的频数直方图即可;
(2)把一组数据按照从小大到或者从大到小的顺序排列,处于最中间位置的数就是中位数,如果是偶数个数据,则最中间两数据的平均数就是中位数,从而判断出中位数落在22万元至26万元收入段内;
(3)这组数据的总和除以这组数据的个数就是这组数据的平均数;
(4)用该小区有1200户住户数![]() 年收入低于18万元的百分比即可。
年收入低于18万元的百分比即可。
【考点精析】本题主要考查了频数分布直方图和算术平均数的相关知识点,需要掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图);总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】第十五届中国“西博会”将于2014年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.
(1)若从这20人中随机选取一人作为联络员,求选到女生的概率;
(2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2、3、4、5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小华做观察水的沸腾实验时所记录的数据:

(1)时间是8分钟时,水的温度为_____;
(2)此表反映了变量_____和_____之间的关系,其中_____是自变量,_____是因变量;
(3)在_____时间内,温度随时间增加而增加;_____时间内,水的温度不再变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB. 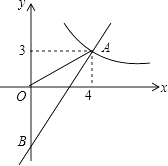
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1:所有评委所给分的平均数,
方案2:在所有评委所给分中,去掉一个最高分和一个最低分.然后再计算其余给分的l平均数.
方案3:所有评委所给分的中位效.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性.先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适台作为这个同学演讲的最后得分,并给出该同学的最后得分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() .
.
(1)![]() ________
________![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(2)如图1,当![]() 为何值时,
为何值时,![]() ?并说明理由;
?并说明理由;

(3)如图2,当点![]() 从点
从点![]() 开始运动,同时,点
开始运动,同时,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,当
运动,当![]() 运动到点
运动到点![]() 或点
或点![]() 运动到点
运动到点![]() 时运动停止.是否存在这样的
时运动停止.是否存在这样的![]() 值,使得
值,使得![]() 与
与![]() 全等?若存在,请求出
全等?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )

A. 110° B. 120° C. 130° D. 140°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com