
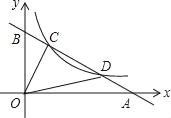
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象相交于C、D两点,和x轴交于A点,y轴交于B点.已知点C的坐标为(3,6),CD=2BC.
(m≠0)的图象相交于C、D两点,和x轴交于A点,y轴交于B点.已知点C的坐标为(3,6),CD=2BC.
(1)求点D的坐标及一次函数的解析式;
(2)求△COD的面积.
【答案】(1)(9,2),y=﹣![]() x+8;(2)24
x+8;(2)24
【解析】
(1)由点C的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数系数m的值,根据比例关系即可找出点D的横坐标,由反比例函数图象上点的坐标特征和m得值即可得出点D的坐标,再结合点C、D的坐标利用待定系数法即可求出一次函数的解析式;
(2)根据一次函数解析式求出点A的坐标,通过分割图形结合三角形的面积公式即可得出结论.
(1)∵反比例函数y![]() (m≠0)过点C(3,6),∴m=3×6=18.
(m≠0)过点C(3,6),∴m=3×6=18.
∵CD=2BC,BD=BC+CD,∴BD=3BC,∴点D的横坐标为3×3=9.
∵点D在反比例函数y![]() 的图象上,∴点D的坐标为(9,2).
的图象上,∴点D的坐标为(9,2).
把点C(3,6)、点D(9,2)代入一次函数y=kx+b(k≠0)中得:
![]() ,解得:
,解得: ,∴一次函数的解析式为y
,∴一次函数的解析式为y![]() x+8.
x+8.
(2)令一次函数y![]() x+8中y=0,则0
x+8中y=0,则0![]() x+8,解得:x=12,即点A的坐标为(12,0),∴S△COD=S△OAC﹣S△OAD
x+8,解得:x=12,即点A的坐标为(12,0),∴S△COD=S△OAC﹣S△OAD![]() OA(yC﹣yD)
OA(yC﹣yD)![]() 12×(6﹣2)=24.
12×(6﹣2)=24.


科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你先认真阅读下列材料,再参照例子解答问题:
已知(x+y﹣3)(x+y+4)=﹣10,求x+y的值.
解:设t=x+y,则原方程变形为(t﹣3)(t+4)=﹣10,即t2+t﹣2=0
∴(t+2)(t﹣1)=0得t1=﹣2,t2=1∴x+y=﹣2或x+y=1
解答问题:(1)已知(x2+y2﹣4)(x2+y2+2)=7,求x2+y2的值.
(2)解方程:x4﹣6x2+8=0
查看答案和解析>>
科目:初中数学 来源: 题型:
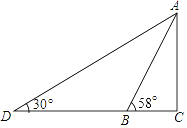
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
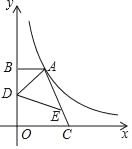
【题目】如图,点A在反比例函数y=![]() 图象的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且EC=
图象的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且EC=![]() AC,点D为OB的中点,若△ADE的面积为5,则k的值为( )
AC,点D为OB的中点,若△ADE的面积为5,则k的值为( )
A. ![]() B. 10 C.
B. 10 C. ![]() D. 12
D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
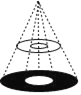
【题目】圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( )
A. 2πm2 B. 3πm2 C. 6πm2 D. 12πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
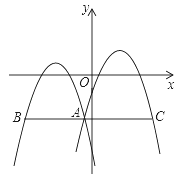
【题目】如图,在平面直角坐标系中,抛物线y=m(x+3)2+n与y=m(x﹣2)2+n+1交于点A.过点A作x轴的平行线,分别交两条抛物线于点B、C(点B在点C左侧),则线段BC的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com