[题目]如图.在中. . .是腰.上的高.交于点．()求证: ．()若.求的度数．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在中，，、是腰、上的高，交于点．

（）求证：．

（）若，求的度数．

【答案】（1）见解析；（2）

【解析】试题分析：（1）首先根据等腰三角形的性质得到∠ABC=∠ACB，然后证明△BEC≌△CDB，得到∠ECB=∠DBC，从而得证；

（2）首先求出∠A的度数，得到∠ACE的度数，进而求出∠COD的度数．

试题解析：解：（1）∵AB=AC，∴∠ABC=∠ACB．

∵BD、CE是△ABC的两条高线，∴∠BEC=∠BDC=90°．

在△BEC和△CDB中，∵∠BEC=∠CDB，∠EBC=∠DCB，BC=CB，∴△BEC≌△CDB，

∴∠DBC=∠ECB，∴OB=OC．

（2）∵∠ABC=65°，AB=AC，∴∠A=180°-2×65°=50°，∴∠ACE=90°－∠A=40°，∴∠COD=90°－∠ACE=90°－40°=50°．

练习册系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】解答题
（1）问题发现
如图1，△ABC和△ADE均为等边三角形，点D在边BC上，连接CE．请填空：
①∠ACE的度数为；
②线段AC、CD、CE之间的数量关系为．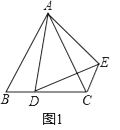

（2）拓展探究
如图2，△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D在边BC上，连接CE．请判断∠ACE的度数及线段AC、CD、CE之间的数量关系，并说明理由．

（3）解决问题
如图3，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD=2，CD=1，AC与BD交于点E，请直接写出线段AC的长度．

查看答案和解析>>

科目：初中数学 来源： 题型：

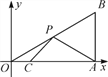
【题目】如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为(3， )，点C的坐标为(，0)，点P为斜边OB上的一个动点，则PA＋PC的最小值为( )

A. B. C. D. 2

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】一块长方体木块的各棱长如图所示，一只蜘蛛在木块的一个顶点A处，一只苍蝇在这个长方体上和蜘蛛相对的顶点B处，蜘蛛急于捉住苍蝇，沿着长方体的表面向上爬．

(1)如果D是棱的中点，蜘蛛沿“AD→DB”路线爬行，它从A点爬到B点所走的路程为多少？

(2)你认为“AD→DB”是最短路线吗？如果你认为不是，请计算出最短的路程．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为调动销售人员的积极性，A、B两公司采取如下工资支付方式：A公司每月2000元基本工资，另加销售额的2%作为奖金；B公司每月1600元基本工资，另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1～6月份的销售额如下表：

(1)请问小李与小张3月份的工资各是多少？

(2)小李1～6月份的销售额与月份的函数关系式是小张1～6月份的销售额也是月份的一次函数，请求出与的函数关系式；

(3)如果7～12月份两人的销售额也分别满足（2）中两个一次函数的关系，问几月份起小张的工资高于小李的工资。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知AB是一段只有3米长的窄道路，由于一辆小汽车与一辆大卡车在AB段相遇，必须倒车才能继续通过．如果小汽车在AB段正常行驶需10分钟，大卡车在AB段正常行驶需20分钟，小汽车在AB段倒车的速度是它正常行驶速度的，大卡车在AB段倒车的速度是它正常行驶的，小汽车需倒车的路程是大卡车的4倍．问两车都通过AB这段狭窄路面的最短时间是分钟．