
【题目】如图1,已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() 和点
和点![]() ,点
,点![]() 在点
在点![]() 的右侧,点
的右侧,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 沿
沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位后得到线段
个单位后得到线段![]() .
.
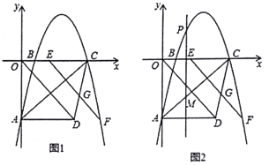
(1)当![]() ______时,点
______时,点![]() 或点
或点![]() 正好移动到抛物线上;
正好移动到抛物线上;
(2)当点![]() 正好移动到抛物线上,
正好移动到抛物线上,![]() 与
与![]() 相交于点
相交于点![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图2,若点![]() 是
是![]() 轴上方抛物线上一动点,过点
轴上方抛物线上一动点,过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() ,探索是否存在点
,探索是否存在点![]() ,使线段
,使线段![]() 长度有最大值?若存在,直接写出点
长度有最大值?若存在,直接写出点![]() 的坐标和
的坐标和![]() 长度的最大值;若不存在,请说明理由.
长度的最大值;若不存在,请说明理由.
【答案】(1)1或2或5;(2)点![]() ;(3)存在点
;(3)存在点![]() ,使线段
,使线段![]() 长度有最大值为5.
长度有最大值为5.
【解析】
(1)分点E与点B重合,点E与点C重合,点F在抛物线上三种情况讨论,可求n的值;
(2)由题意可求直线EF解析式,直线CD解析式,即可求点G坐标;
(3)由题意可求直线AC解析式,设点P(t,-![]() t2+
t2+![]() t-4),则点M(t,
t-4),则点M(t,![]() t-4),则可用t表示PM的长度,根据二次函数的性质可求点P的坐标.
t-4),则可用t表示PM的长度,根据二次函数的性质可求点P的坐标.
解:(1)∵抛物线![]() 与x轴相交于B和点C
与x轴相交于B和点C
∴![]()
解得:x1=1,x2=5
∴点B(1,0),点C(5,0)
当点E与点B重合,则n=1,
当点E与点C重合,则n=5
当点F在抛物线上,则![]()
解得:x1=0(不合题意舍去),x2=6
∴F(6,-4)
∴n=6-4=2
故答案为:1或2或5;
(2)∵点![]() 正好移动到抛物线上
正好移动到抛物线上
∴![]()
∴点![]() 坐标为
坐标为![]()
设直线![]() 解析式为
解析式为![]() ,把点
,把点![]() ,点
,点![]() 代入解析式得
代入解析式得
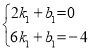 ,解得
,解得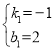
∴直线![]() 解析式为:
解析式为:![]()
设直线CD解析式为![]() ,把点
,把点![]() ,点
,点![]() 代入解析式得
代入解析式得
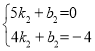 ,解得
,解得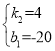
∴直线![]() 解析式
解析式![]()
∵![]() 与
与![]() 相交于点
相交于点![]() ,设点
,设点![]()
![]() ,解得:
,解得: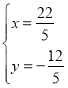
∴点![]() ,
,
(3)∵抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,
∴当![]() 时,
时,![]()
∴点![]()
∵点![]() ,点
,点![]()
∴直线![]() 解析式:
解析式:![]() ,
,
设点![]() ,则点
,则点![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 的最大值为5
的最大值为5
∴点![]() 坐标为
坐标为![]() ,
,
∴存在点![]() ,使线段
,使线段![]() 长度有最大值为5.
长度有最大值为5.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】疫情防控形势下,人们在外出时都应戴上口罩以保护自己免受新型冠状病毒感染.某药店用4000元购进若干包一次性医用口罩,很快售完,该店又用![]() 元钱购进第二批这种口罩,所进的包数比第一批多
元钱购进第二批这种口罩,所进的包数比第一批多![]() ,每包口罩的进价比第一批每包口罩的进价多
,每包口罩的进价比第一批每包口罩的进价多![]() 元,请解答下列问题:
元,请解答下列问题:

![]() 求购进的第一批医用口罩有多少包;
求购进的第一批医用口罩有多少包;
![]() 政府采取措施,在这两批医用口罩的销售中,售价保持了一致.若售完这两批口罩的总利润不高于
政府采取措施,在这两批医用口罩的销售中,售价保持了一致.若售完这两批口罩的总利润不高于![]() 元钱,那么药店销售该口罩每包的最高售价是多少元?
元钱,那么药店销售该口罩每包的最高售价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
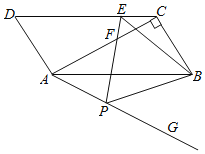
【题目】如图,在ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2![]() ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,则AF=_____.
,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,则AF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
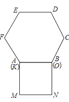
【题目】已知正方形![]() 和正六边形
和正六边形![]() 边长均为1,如图所示,把正方形放置在正六边形外,使
边长均为1,如图所示,把正方形放置在正六边形外,使![]() 边与
边与![]() 边重合,按下列步骤操作:将正方形在正六边形外绕点
边重合,按下列步骤操作:将正方形在正六边形外绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第一次旋转;再绕点
边重合,完成第一次旋转;再绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第二次旋转;此时点
边重合,完成第二次旋转;此时点![]() 经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点
经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点![]() ,
,![]() 之间距离的最大值是______.
之间距离的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,与y轴交于点C,且OA=OC.
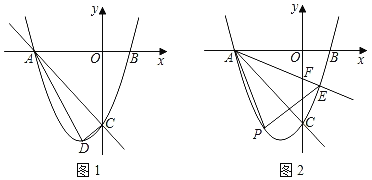
(1)求抛物线的解析式;
(2)点D是抛物线顶点,求△ACD的面积;
(3)如图2,射线AE交抛物线于点E,交y轴的负半轴于点F(点F在线段AE上),点P是直线AE下方抛物线上的一点,S△ABE=![]() ,求△APE面积的最大值和此动点P的坐标.
,求△APE面积的最大值和此动点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组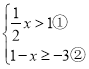
请结合题意,完成本题解答.
(1)解不等式①,得_________________;
(2)解不等式②,得:_________________;
(3)原不等式组的解集为_________________;
(4)把不等式组的解集在数轴上表示出来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
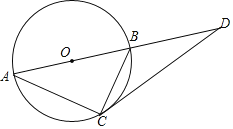
【题目】如图,已知AB是⊙O的直径,DC与⊙O相切于点C,交AB的延长线于点D.
(1)求证:∠BAC=∠BCD;
(2)若BD=4,DC=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (k>0)与一次函数
(k>0)与一次函数![]() 的图象相交于两点A(
的图象相交于两点A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),线段AB交y轴与C,当|
),线段AB交y轴与C,当|![]() -
-![]() |=2且AC = 2BC时,k、b的值分别为( )
|=2且AC = 2BC时,k、b的值分别为( )

A. k=![]() ,b=2 B. k=
,b=2 B. k=![]() ,b=1 C. k=
,b=1 C. k=![]() ,b=
,b=![]() D. k=
D. k=![]() ,b=
,b=![]()
【答案】D
【解析】∵AC=2BC,∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.∵点A、点B都在一次函数y=x+b的图象上,∴设B(m, ![]() m+b),则A(-2m,-m+b),∵|
m+b),则A(-2m,-m+b),∵|![]() -
-![]() |=2,∴m-(-2m)=2,解得m=
|=2,∴m-(-2m)=2,解得m=![]() ,又∵点A、点B都在反比例函数
,又∵点A、点B都在反比例函数![]() 的图象上,∴
的图象上,∴![]() (
(![]() +b)=(-
+b)=(-![]() )×(-
)×(-![]() +b),解得b=
+b),解得b=![]() ,∴k=
,∴k=![]() ×(
×(![]() +
+![]() )=
)=![]() ,故选D.
,故选D.
【题型】单选题
【结束】
11
【题目】若点(4,m)在反比例函数![]() (x≠0)的图象上,则m的值是 .
(x≠0)的图象上,则m的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com