
【题目】如图,在ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2![]() ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,则AF=_____.
,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,则AF=_____.
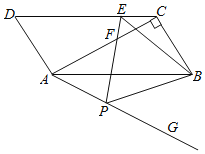
【答案】![]()
【解析】
如图,连接PC交AB于T,作PN⊥AB于N,CM⊥PC交PE的延长线于M.首先证明∠APC=90°,解直角三角形求出AC,PA,利用相似三角形的性质求出CM,由CM∥PA,推出![]() ,由此即可解决问题.
,由此即可解决问题.
解:如图,连接PC交AB于T,作PN⊥AB于N,CM⊥PC交PE的延长线于M.
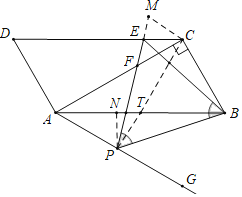
∵AC⊥BC,
∴∠ACB=90°,
∵BC=![]() ,∠BAC=30°,
,∠BAC=30°,
∴AB=2BC=![]() ,AC=
,AC=![]() BC=6,∠ABC=60°,
BC=6,∠ABC=60°,
∵∠EPB=∠EBP=60°,
∴△EPB是等边三角形,
∴∠PEB=60°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BCE=180°﹣∠ABC=120°,
∴∠EPB+∠BCE=180°,
∴P,B,C,E四点共圆,
∴∠PCB=∠PEB=60°,∠MPC=∠EBC,
∵∠TCB=∠CBT=60°
∴△TCB是等边三角形,
∴∠BCT=60°,∠ACT=30°,BT=BC=AT=![]() ,
,
∵∠BAG=∠BAC=30°,
∴∠APC=90°,
∴PA=ATcos30°=3,AN=PAcos30°=![]() ,PN=
,PN=![]() PA=
PA=![]() ,PC=
,PC=![]() PA=
PA=![]() ,
,
∴BN=AB﹣AN=![]() ,
,
∵∠PBE=∠CBT=60°,
∴∠PBN=∠CBE=∠CPM,
∵∠PCM=∠PNB=90°,
∴△PCM∽△BNP,
∴![]() ,
,
∴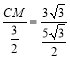 ,
,
∴CM=![]() ,
,
∵PA⊥PC,CM⊥PC,
∴CM∥PA,
∴ ,
,
∴AF=![]() AC=
AC=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】某班甲、乙、丙、丁四位同学周一到周四轮流值日.
(1)若每个同学只随机值日一天,则甲恰好在周一值日的概率是多少?
(2)若每两个同学为一组,四位同学被分成两组.
①甲分在第一组的概率为
②求甲、乙同时分在第一组的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视机厂要印制产品宣传材料甲印刷厂提出:每份材料收1元印制费,另需收取所有印制材料的制版费1500元;乙印刷厂提出:每份材料收2.5元印制费,不收制版费.设该电视厂在同一个印刷厂一次印的数量为![]() 份
份![]() .
.
(1)根据题意填表:
一次印制数量(份) | 300 | 500 | 1500 | … |
甲印刷厂花费(元) | 2000 | … | ||
乙印刷厂花费(元) | 1250 | … |
(2)设在甲印刷厂花费![]() 元,在乙印刷厂花费
元,在乙印刷厂花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若电视厂在甲印刷厂和在乙印刷厂一次印制宣传材料的数量相同,且花费相同,则该电视厂在同一个印刷厂一次印制材料的数量为 份;
②印制800份宣传材料时,选择 印刷厂比较合算;
③电视机厂拟拿出3000元用于印制宣传材料,在 印刷厂印制宣传材料可以多一些.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并解决问题.
一道习题引发的思考
小明在学习《勾股定理》一章内容时,遇到了一个习题,并对有关内容进行了研究;
习题再现:
古希腊的哲学家柏拉图曾指出,如果![]() 表示大于1的整数,
表示大于1的整数,![]() ,
,![]() ,
,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
资料搜集:
定义:勾股数是指可以构成一个直角三角形三边的一组正整数.一般地,若三角形三边长![]() ,
,![]() ,
,![]() 都是正整数,且满足
都是正整数,且满足![]() ,那么
,那么![]() ,
,![]() ,
,![]() 称为一组勾股数.
称为一组勾股数.
关于勾股数的研究:我囯西周初数学家商高在公元前1000年发现了“勾三,股四,弦五”,这组数![]() 是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:
是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:![]() ,
,![]() ,
,![]()
![]() ,其中
,其中![]() ,
,![]() ,
,![]() 是互质的奇数.(注:
是互质的奇数.(注:![]() ,
,![]() ,
,![]() 的相同倍数组成的一组数也是勾股数)
的相同倍数组成的一组数也是勾股数)

问题解答:
(1)根据柏拉图的研究,当![]() 时,请直接写出一组勾股数;
时,请直接写出一组勾股数;
(2)若![]() 表示大于1的整数,试证明
表示大于1的整数,试证明![]() 是一组勾股数;
是一组勾股数;
(3)请举出一个反例(即写出一组勾股数),说明柏拉图给出的勾股数公式不能构造出所有的勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接了60万平方米的绿化工程,由于情况有变,…设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省路的部分是( )
,根据方程可知省路的部分是( )
A.实际每天的工作效率比原计划提高了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
B.实际每天的工作效率比原计划提高了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
C.实际每天的工作效率比原计划降低了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
D.实际每天的工作效率比原计划降低了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() 和点
和点![]() ,点
,点![]() 在点
在点![]() 的右侧,点
的右侧,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 沿
沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位后得到线段
个单位后得到线段![]() .
.
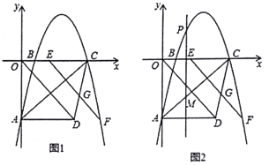
(1)当![]() ______时,点
______时,点![]() 或点
或点![]() 正好移动到抛物线上;
正好移动到抛物线上;
(2)当点![]() 正好移动到抛物线上,
正好移动到抛物线上,![]() 与
与![]() 相交于点
相交于点![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图2,若点![]() 是
是![]() 轴上方抛物线上一动点,过点
轴上方抛物线上一动点,过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() ,探索是否存在点
,探索是否存在点![]() ,使线段
,使线段![]() 长度有最大值?若存在,直接写出点
长度有最大值?若存在,直接写出点![]() 的坐标和
的坐标和![]() 长度的最大值;若不存在,请说明理由.
长度的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点
的顶点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() 于点
于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,连接
,连接![]() .
.
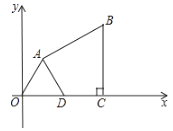
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)求点![]() 的坐标;
的坐标;
(3)平行于![]() 的直线
的直线![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向平移.设直线
轴正方向平移.设直线![]() 被四边形
被四边形![]() 截得的线段长为
截得的线段长为![]() ,直线
,直线![]() 与
与![]() 轴交点的横坐标为
轴交点的横坐标为![]() .
.
①当直线![]() 与
与![]() 轴的交点在线段
轴的交点在线段![]() 上(交点不与点
上(交点不与点![]() 重合)时,请直接写出
重合)时,请直接写出![]() 与
与![]() 的函数关系式(不必写出自变量
的函数关系式(不必写出自变量![]() 的取值范围)
的取值范围)
②若![]() ,请直接写出此时直线
,请直接写出此时直线![]() 与
与![]() 轴的交点坐标.
轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
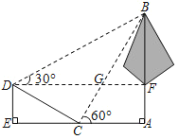
A.10B.15C.15![]() D.15
D.15![]() ﹣5
﹣5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com