
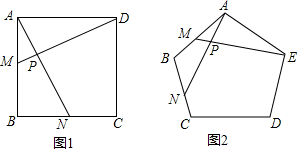
分析 (1)由正方形的性质得出AD=AB,∠DAM=∠ABN=90°,由SAS证明△ADM≌△BAN,得出∠ADM=∠BAN,即可得出结果;
(2)由正五边形的性质得出AB=AE,∠EAM=∠ABN=108°,由SAS证明△AEM≌△BAN,得出∠AEM=∠BAN,由三角形的外角性质和三角形内角和定理求出∠APE的度数,即可得出结果.
解答 (1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAM=∠ABN=90°,
∴∠BAN+∠DAP=90°,
在△ADM和△BAN中,
$\left\{\begin{array}{l}{AD=AB}&{\;}\\{∠DAM=∠ABN}&{\;}\\{AM=BN}&{\;}\end{array}\right.$,
∴△ADM≌△BAN(SAS),
∴∠ADM=∠BAN,
∴∠DPN=∠ADM+∠DAP=∠BAN+∠DAP=90°;
(2)解:∵五边形ABCDE是正五边形,
∴AB=AE,∠EAM=∠ABN=108°,
在△AEM和△BAN中,
$\left\{\begin{array}{l}{AE=AB}&{\;}\\{∠EAM=∠ABN}&{\;}\\{AM=BN}&{\;}\end{array}\right.$,
∴△AEM≌△BAN(SAS),
∴∠AEM=∠BAN,
∵∠APE=∠AME+∠BAN=∠AEM+∠AME=180°-108°=72°,
∴∠EPN=180°-72°=108°.
点评 本题考查了全等三角形的判定与性质、正方形的性质、正五边形的性质;熟练掌握正方形和正五边形的性质,证明三角形全等是解决问题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB∥CD,∠A=∠D=60°,AC与BD交于点E,连接BC,其中点M,N,K 分别是AE,BC,DE边上的中点.求证:NK=MN.
如图,AB∥CD,∠A=∠D=60°,AC与BD交于点E,连接BC,其中点M,N,K 分别是AE,BC,DE边上的中点.求证:NK=MN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
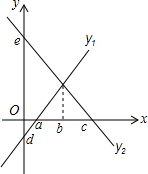 如图,先观察图形,然后填空:
如图,先观察图形,然后填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作出函数y1=2x-2与y2=-2x+6的图象,利用图象解答下列问题:
作出函数y1=2x-2与y2=-2x+6的图象,利用图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
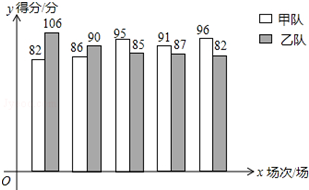 甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)| 平均数 | 中位数 | 方差 | |
| 甲 | 90 | 91 | 28.4 |
| 乙 | 90 | 87 | 70.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每月用水量 | 单价 |
| 不超出10立方米的部分 | 2元/立方米 |
| 超出10立方米 | 3元/立方米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com