Question

7．如图，AB∥CD，∠A=∠D=60°，AC与BD交于点E，连接BC，其中点M，N，K 分别是AE，BC，DE边上的中点．求证：NK=MN．

Answer 1

分析 取BE的中点E，CE的中点F，连结MG、NG、NF、KF，如图，先判断△ABE和△CDE都是等边三角形得到AB=BE，CD=CE，再根据三角形中位线性质得到MG=$\frac{1}{2}$AB，MG∥AB，FN=$\frac{1}{2}$BE，FN∥BE，NG=$\frac{1}{2}$CE，NG∥CE，KF=$\frac{1}{2}$CD，KF∥CD，则MG=NF，NG=KF，根据平行线的性质得∠NGE=∠GEM=∠EFN，易得∠MGN=∠NFK，则根据“SAS”可判断△GMN≌△FNK，所以MN=NK．

解答 证明：取BE的中点E，CE的中点F，连结MG、NG、NF、KF，如图，
∵AB∥CD，
∴∠A=∠ACD=60°，∠ABD=∠D=60°，
∴△ABE和△CDE都是等边三角形，
∴AB=BE，CD=CE，
∵点M，N，K、G，F分别是AE，BC，DE，BE，CE边上的中点，
∴MG=$\frac{1}{2}$AB，MG∥AB，FN=$\frac{1}{2}$BE，FN∥BE，NG=$\frac{1}{2}$CE，NG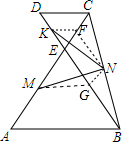∥CE，KF=$\frac{1}{2}$CD，KF∥CD，
∴MG=NF，NG=KF，∠NGE=∠GEM=∠EFN，
而∠EGM=∠ABE=60°，∠EFK=∠ECD=60°，
∴∠MGN=∠NFK，
在△GMN和△FNK中，
$\left\{\begin{array}{l}{MG=FN}\\{∠MGN=∠NFK}\\{GN=FK}\end{array}\right.$，
∴△GMN≌△FNK，
∴MN=NK．

点评 本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．也考查了等边三角形的判定与性质．构建三角形中位线和运用三角形中位线性质是解决此题的关键．