
)如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
(1)求证:AD是⊙O的切线;
(2)连接OC,交⊙O于点G,若AB=4,求线段CE、CG与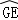 围成的阴影部分的面积S.
围成的阴影部分的面积S.
科目:初中数学 来源: 题型:
本溪市高新区2015年1月份公共财政预算收入完成259 610 000元,首月实现税收收入“开门红”.将259 610 000用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知矩形ABCD的边长分别为a,b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形In,则In的面积是 .
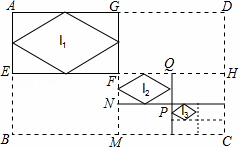
查看答案和解析>>
科目:初中数学 来源: 题型:
购买1个单价为a元的面包和3瓶单价为b元的饮料,所需钱数为( )
A. (a+b)元 B. 3(a+b)元 C. (3a+b)元 D. (a+3b)元
查看答案和解析>>
科目:初中数学 来源: 题型:
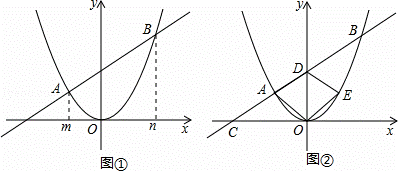
如图①,一次函数y=kx+b的图象与二次函数y=x2的图象相交于A,B两点,点A,B的横坐标分别为m,n(m<0,n>0).
(1)当m=﹣1,n=4时,k= ,b= ;
当m=﹣2,n=3时,k= ,b= ;
(2)根据(1)中的结果,用含m,n的代数式分别表示k与b,并证明你的结论;
(3)利用(2)中的结论,解答下列问题:
如图②,直线AB与x轴,y轴分别交于点C,D,点A关于y轴的对称点为点E,连接AO,OE,ED.
①当m=﹣3,n>3时,求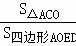 的值(用含n的代数式表示);
的值(用含n的代数式表示);
②当四边形AOED为菱形时,m与n满足的关系式为 n=﹣2m ;
当四边形AOED为正方形时,m= ﹣1 ,n= 2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com