
【题目】如图,在正方形ABCD的外侧, 作两个等腰三角形ADE和DCF,
(1) 若EA=ED=FD=FC,请判断BE和AF的关系?并给予证明.
(2)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,请用备用图画出图形,直接写出BE和AF的关系,不用证明.
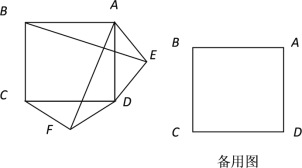
【答案】(1)AF=BE,AF⊥BE,理由见解析(2)AF=BE,AF⊥BE,理由见解析
【解析】
(1)根据正方形的性质、等腰三角形的性质以及全等三角形的判定定理证明△BAE≌△ADF,根据全等三角形的性质进行证明;
(2)同(1)一样的方法证明即可.
(1)在正方形ABCD中,∠BAD=∠ADC=90![]() ,AB=AD=CD.
,AB=AD=CD.
∵EA=ED=FD=FC,
在△AED和△DFC中,
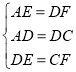 ,
,
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.
即∠BAE=∠ADF.
在△BAE和△ADF中,
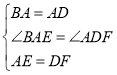 ,
,
∴△BAE≌△ADF(SAS)
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90![]() ,
,
∴∠ABE+∠BAF=90![]() ,
,
∴∠AMB=90![]() ,
,
∴AF⊥BE.
故AF=BE,AF⊥BE.

(2)所画图形如图,AF=BE,AF⊥BE理由如下:
在△AED和△DFC中,
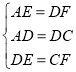 ,
,
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.即∠BAE=∠ADF.
在△BAE和△ADF中,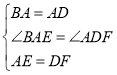 ,
,
∴△BAE≌△ADF(SAS),
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90![]() ,
,
∴∠ABE+∠BAF=90![]() ,
,
∴∠AMB=90![]() ,
,
∴AF⊥BE.
故AF=BE,AF⊥BE.


科目:初中数学 来源: 题型:
【题目】某数学拓展课研究小组经过市场调查,发现某种衣服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件160元,售价为x元,月销量为y件.
(1)求出y关于x的函数关系式;
(2)若销售该运动服的月利润为w元,求出w关于x的函数关系式,并求出月利润最大时的售价;
(3)由于运动服进价降低了a元,商家决定回馈顾客,打折销售,结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低10元,则a的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
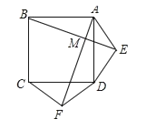
【题目】已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,设AM=x,BN=y,记△ADM的面积为S1,△BND的面积为S2.
(1)如图(1),当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,S1S2= ;
(2)在(1)的条件下,将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转如图(2)所示位置,
①求y与x的函数关系式;②求S1S2的值;
(3)当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α,如图(3),当点D在BA的延长线上运动时,设的AD=a,BD=b,直接写出S1S2的关系式(用含a、b和α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,∠BAC=120°,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
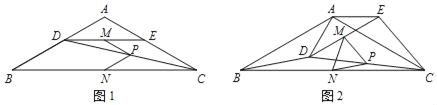
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,∠MPN的度数是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=8,请直接写出△PMN面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.
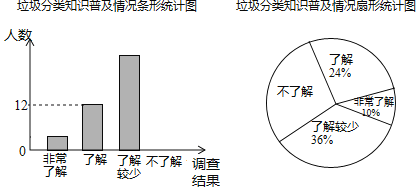
(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 XOY中,对于任意两点 ![]() (
(![]() ,
,![]() )与
)与 ![]() (
(![]() ,
,![]() )的“非常距离”,给出如下定义: 若
)的“非常距离”,给出如下定义: 若 ![]() ,则点
,则点 ![]() 与点
与点 ![]() 的“非常距离”为
的“非常距离”为 ![]() ;若
;若 ![]() ,则点
,则点 ![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为 ![]() .
.
例如:点 ![]() (1,2),点
(1,2),点 ![]() (3,5),因为
(3,5),因为 ![]() ,所以点
,所以点 ![]() 与点
与点 ![]() 的“非常距离”为
的“非常距离”为 ![]() ,也就是图1中线段
,也就是图1中线段 ![]() Q与线段
Q与线段 ![]() Q长度的较大值(点 Q为垂直于 y轴的直线
Q长度的较大值(点 Q为垂直于 y轴的直线 ![]() Q与垂直于 x轴的直线
Q与垂直于 x轴的直线 ![]() Q的交点)。
Q的交点)。
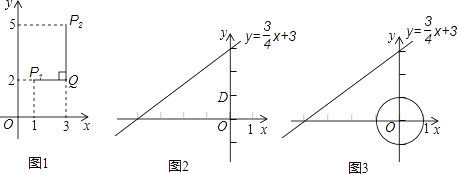
(1)已知点 A(-![]() ,0), B为 y轴上的一个动点,①若点 A与点 B的“非常距离”为2,写出一个满足条件的点 B的坐标;②直接写出点 A与点 B的“非常距离”的最小值;
,0), B为 y轴上的一个动点,①若点 A与点 B的“非常距离”为2,写出一个满足条件的点 B的坐标;②直接写出点 A与点 B的“非常距离”的最小值;
(2)已知 C是直线 ![]() 上的一个动点,①如图2,点 D的坐标是(0,1),求点 C与点 D的“非常距离”的最小值及相应的点 C的坐标; ②如图3, E是以原点 O为圆心,1为半径的圆上的一个动点,求点 C与点 E的“非常距离”的最小值及相应的点 E和点 C的坐标。
上的一个动点,①如图2,点 D的坐标是(0,1),求点 C与点 D的“非常距离”的最小值及相应的点 C的坐标; ②如图3, E是以原点 O为圆心,1为半径的圆上的一个动点,求点 C与点 E的“非常距离”的最小值及相应的点 E和点 C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂用![]() 天时间生产一款新型节能产品,每天生产的该产品被某网店以每件
天时间生产一款新型节能产品,每天生产的该产品被某网店以每件![]() 元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第
元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第![]() 天的生产成本
天的生产成本![]() (元/件)与
(元/件)与![]() (天)之间的关系如图所示,第
(天)之间的关系如图所示,第![]() 天该产品的生产量
天该产品的生产量![]() (件)与
(件)与![]() (天)满足关系式
(天)满足关系式![]()
![]() 第
第![]() 天,该厂生产该产品的利润是 元;
天,该厂生产该产品的利润是 元;
![]() 设第
设第![]() 天该厂生产该产品的利润为
天该厂生产该产品的利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在生产该产品的过程中,当天利润不低于![]() 元的共有多少天?
元的共有多少天?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.
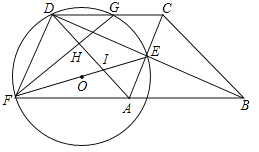
(1)求∠FDE的度数;
(2)试判断四边形FACD的形状,并证明你的结论;
(3)当G为线段DC的中点时,
①求证:FD=FI;
②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com