
【题目】如图,抛物线y=-x2+bx+c的顶点为C(3,4),交x轴于点A,B(点B在点A的右侧),点P在第一象限,且在抛物线AC部分上,PD⊥PC交x轴于点D。
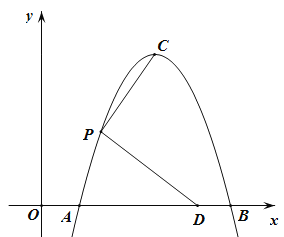
(1)求该抛物线的表达式;
(2)若PD=3PC,求OD的长.
【答案】(1)y=-x2+6x-5;(2)OD= 5.
【解析】
(1)已知顶点坐标,现知a值,直接用顶点法即可求出抛物线的解析式;
(2)先求出抛物线与x轴的交点坐标,设P(p,-![]() +6p-5)(1≤p≤3),先证明△Rt△PCF∽Rt△PED,根据相似三角形的性质列比例式,求出p值,然后根据C、F两点的纵坐标,求得CF的长,则由相似的性质即可得出ED的长,则OD的长可知.
+6p-5)(1≤p≤3),先证明△Rt△PCF∽Rt△PED,根据相似三角形的性质列比例式,求出p值,然后根据C、F两点的纵坐标,求得CF的长,则由相似的性质即可得出ED的长,则OD的长可知.
解:
(1)由题意得,y=-(x-3)2+4=-x2+6x-5;
(2)设y=-x2+6x-5=(x-1)(-x+5)=0,
解得x=1或5,
∴A(1,0),B(5,0),
如图,过点P作PE∥y轴交x轴于点E,过P作PF平行x轴交对称轴于F,
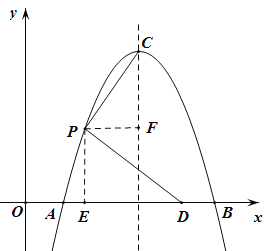
设P(p,-p2+6p-5)(1≤p≤3),
∴∠PFC=∠PED=90°
∵∠CPF+∠FPD=∠EPD+∠FPD=90°,
∵∠CPF=∠DPE,
∴∠PFC=∠PDE,
又∵∠PFC=∠PED=90°
∴Rt△PCF∽Rt△PDE,
∴![]() ,
,
∴![]() ,ED=3CF
,ED=3CF
整理得p2-9p+14=0,
(p-2)(p-7)=0,
∴p=2, 或P=7(舍去),
∴P(2,3),
CF=yC-yF=4-3=1,
∴ED=3CF=3,
∴OD=OE+ED=2+3=5.


科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度,2011年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2013年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2013年底共建设了多少万平方米廉租房.
查看答案和解析>>
科目:初中数学 来源: 题型:
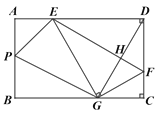
【题目】如图,在矩形ABCD中,点E,F分别在边AD,DC上,AB=6,DF=4,将矩形沿直线EF折叠,点D恰好落在BC边上的点G处,连接DG交EF于点H.
(1)求DE的长度.
(2)求![]() 的值.
的值.
(3)若AB边上有且只存在2个点P,使△APE与△BPG相似,请直接写出边AD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶销售商计划将m罐茶叶按甲、乙两种礼品盒包装出售,其中甲种礼品盒每盒装4罐,每盒售价240元;乙种礼品盒每盒装6罐,每盒售价300元,恰好全部装完.已知每罐茶叶的成本价为30元,设甲种礼品盒的数量为x盒,乙种礼品盒的数量为y盒.
(1)当m=120时.
①求y关于x的函数关系式.
②若120罐茶叶全部售出后的总利润不低于3000元,则甲种礼品盒的数量至少要多少盒?
(2)若m罐茶叶全部售出后平均每罐的利润恰好为24元,且甲、乙两种礼品盒的数量和不超过69盒,求m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
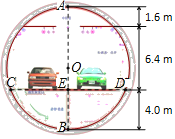
【题目】如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为实数,关于x的方程为x2+(k+2)x+2k=1.
(1)判断方程有无实数根.
(2)当方程的根和k都是有理数时,请直接写出其中k的1个值和相应方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com