
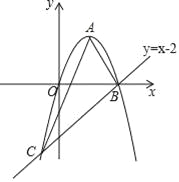
【题目】如图,已知抛物线y=﹣x2+2x经过原点O,且与直线y=x﹣2交于B,C两点.
(1)求抛物线的顶点A的坐标及点B,C的坐标;
(2)求证:∠ABC=90°;
(3)在直线BC上方的抛物线上是否存在点P,使△PBC的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
【答案】(1) A(1,1) ,B(2,0),C(﹣1,﹣3) (2)见解析 (3)(![]() ,
,![]() )
)
【解析】(1)把抛物线解析式化为顶点式可求得A点坐标,联立抛物线与直线的解析式可求得B、C的坐标;
(2)由A、B、C的坐标可求得AB2、BC2和AC2,由勾股定理的逆定理可判定△ABC是直角三角形;
(3)过点P作PG∥y轴,交直线BC于点G,设出P点坐标,则可表示出G点坐标,从而可表示出PG的长,则可表示出△PBC的面积,利用二次函数的性质可求得其最大值时P点坐标.
(1)∵y=-x2+2x=-(x-1)2+1,
∴抛物线顶点坐标A(1,1),
联立抛物线与直线解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴B(2,0),C(-1,-3);
(2)证明:
由(1)可知B(2,0),C(-1,-3),A(1,1),
∴AB2=(1-2)2+12=2,BC2=(-1-2)2+(-3)2=18,AC2=(-1-1)2+(-3-1)2=20,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,
∴∠ABC=90°;
(3)如图,过点P作PG∥y轴,交直线BC于点G,
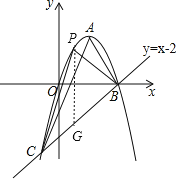
设P(t,-t2+2t),则G(t,t-2),
∵点P在直线BC上方,
∴PG=-t2+2t-(t-2)=-t2+t+2=-(t-![]() )2+
)2+![]() ,
,
∴S△PBC=S△PGB+S△PGC=![]() PG[2-(-1)]=
PG[2-(-1)]=![]() PG=-
PG=-![]() (t-
(t-![]() )2+
)2+![]() ,
,
∵-![]() <0,
<0,
∴当t=![]() 时,S△PBC有最大值,此时P点坐标为(
时,S△PBC有最大值,此时P点坐标为(![]() ,
,![]() ),
),
即存在满足条件的点P,其坐标为(![]() ,
,![]() )
)


科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上,从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t秒。
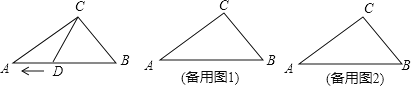
(1)点D在运动t秒后,BD= cm(用含有t的式子表示)
(2)AB=cm,AB边上的高为cm;
(3)点D在运动过程中,当△BCD为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|=|a﹣b|.
理解:
(1)数轴上表示2和﹣3的两点之间的距离是 ;
(2)数轴上表示x和﹣5的两点A和B之间的距离是 ;
(3)当代数式|x﹣1|+|x+3|取最小值时,相应的x的取值范围是 ;最小值是 .
应用:某环形道路上顺次排列有四家快递公司:A、B、C、D,它们顺次有快递车16辆,8辆,4辆,12辆,为使各快递公司的车辆数相同,允许一些快递公司向相邻公司调出,问共有多少种调配方案,使调动的车辆数最少?并求出调出的最少车辆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=12,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM?
(2)当P在线段AB上运动时,试说明2BM﹣BP为定值.
(3)当P在AB延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变,选择一个正确的结论,并求出其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为33°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?(结果用含非特殊角的三角函数和根式表示即可)
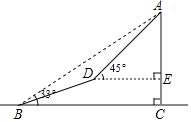
查看答案和解析>>
科目:初中数学 来源: 题型:
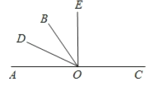
【题目】如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,且∠DOE=60°,∠BOE=![]() ∠EOC,则下列四个结论正确的有__________
∠EOC,则下列四个结论正确的有__________
①∠BOD=30°;②射线OE平分∠AOC;③图中与∠BOE互余的角有2个;④图中互补的角有6对.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com