【题目】某日6时至10时，某交易平台上一种水果的每千克售价、每千克成本与交易时间之间的关系分别如图1、图2所示（图1、图2中的图象分别是线段和抛物线，其中点P是抛物线的顶点）.在这段时间内，出售每千克这种水果收益最大的时刻是_____ ，此时每千克的收益是_________
名校课堂系列答案科目：初中数学 来源： 题型：
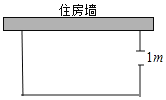
【题目】如图，一农户要建一个矩形猪舍，猪舍的一边利用长为15m的住房墙，另外三边用27m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长，宽分别为多少米时，猪舍面积为96m2？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连接AD．
①AD_____AN（填“＞”，“＝”或“＜”）；
②AB＝8，ON＝1，⊙O的半径为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，P是直线y＝2上的一个动点，⊙P的半径为1，直线OQ切⊙P于点Q，则线段OQ取最小值时，Q点的坐标为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
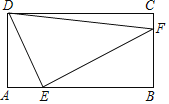
【题目】如图，点E是矩形ABCD边AB上一动点（不与点B重合），过点E作EF⊥DE交BC于点F，连接DF，已知AB＝4cm，AD＝2cm，设A，E两点间的距离为xcm，△DEF面积为ycm2．
小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小明的探究过程，请补充完整：
（1）确定自变量x的取值范围是 ；
（2）通过取点、画图、测量、分析，得到了x与y的几组值，如表：
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y/cm2 | 4.0 | 3.7 | 3.9 | 3.8 | 3.3 | 2.0 | … |
（说明：补全表格时相关数值保留一位小数）
（3）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（4）结合画出的函数图象，解决问题：当△DEF面积最大时，AE的长度为 cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
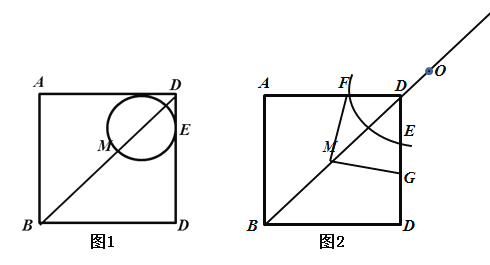
【题目】已知正方形ABCD的边长为2，中心为M，⊙O的半径为r，圆心O在射线BD上运动，⊙O与边CD仅有一个公共点E.
（1）如图1，若圆心O在线段MD上，点M在⊙O上，OM=DE，判断直线AD与⊙O的位置关系，并说明理由；
（2）如图2，⊙O与边AD交于点F，连接MF，过点M作MF的垂线与边CD交于点G，若
，设点O与点M之间的距离为
,EG=
,当
时，求
的函数解析式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
经过点A（1,0），B（4,0）与
轴交于点C．
（1）求抛物线的解析式；
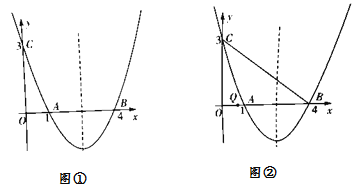
（2）如图①，在抛物线的对称轴上是否存在点P，使得四边形PAOC的周长最小？若存在，求出四边形PAOC周长的最小值；若不存在，请说明理由．
（3）如图②，点Q是线段OB上一动点，连接BC，在线段BC上是否存在这样的点M，使△CQM为等腰三角形且△BQM为直角三角形？若存在，求M的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
与双曲线
相交于点
.
（1）求反比例函数的表达式：
（2）画出直线和双曲线的示意图；
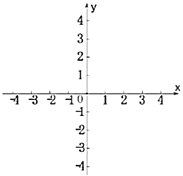
（3）直接写出
的解集______；
（4）若点
是坐标轴负半轴上一点，且满足
.直接写出点的坐标______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表.为了节约资金,小明应选择哪一种购买方案?请说明理由.
大笔记本 | 小笔记本 | |
价格(元/本) | 6 | 5 |
页数(页/本) | 100 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
