
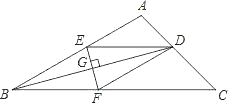
【题目】如图,在 ABC 中,BD 平分ABC 交 AC 于 D ,EF 垂直平分 BD ,分别交 AB, BC, BD于 E, F , G ,连接 DE, DF 。
(1)求证:四边形 BEDF 为菱形;
(2)若ABC 30, C 45, DE 4 ,求CF 的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)先根据垂直平分线的性质得:DE=BE,DF=FB,证明△BEG≌△BFG(ASA),根据对角线互相平分的四边形是平行四边形得:四边形DFBE是平行四边形,再由一组邻边相等的平行四边是菱形可得结论;
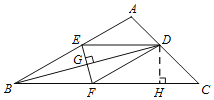
(2)过D作DH⊥CF于H.在Rt△DFH中,求出DH、FH,在Rt△DHC中,求出CH即可解决问题;
(1)证明:∵EF是BD的垂直平分线,
∴DE=EB,DF=BF,∠EGB=∠FGB=90°,DG=BG
∵BD平分∠ABC,
∴∠EBG=∠FBG,
∵BG=BG,
∴△BEG≌△BFG(ASA),
∴GE=GF,
∴四边形DFBE是平行四边形,
∵DE=BE,
∴四边形DFBE是菱形;
(2)解:过D作DH⊥CF于H.
∵四边形BFDE是菱形,
∴DF∥AB,DE=DF=4.
在Rt△DFH中,∠DFC=∠ABC=30°,
![]()
在Rt△CDH中,∠C=45°,
∴DH=HC=2,
![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,作抛物线
中,作抛物线![]() 关于
关于![]() 轴对称的抛物线
轴对称的抛物线![]() ,再将抛物线
,再将抛物线![]() 向左平移2个单位,向上平移1个单位,得到的抛物线
向左平移2个单位,向上平移1个单位,得到的抛物线![]() 的函数解析式是
的函数解析式是![]() ,则抛物线
,则抛物线![]() 所对应的的函数解析式是( )
所对应的的函数解析式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
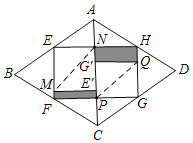
【题目】在关于“折纸问题”的数学活动课中,小刚沿菱形纸片ABCD各边中点的连线裁剪得到四边形纸片EFGH,再将纸片EFGH按如图所示分别沿MN、P2折叠,使点E,G落在线段PN上点E,G处,当PNEF时,若阴影部分的周长之和为16,△AEH,△CFG的面积之和为12,则菱形纸片ABCD的一条对角线BD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为3的正方形ABCD中,点E是BC边上的点,EC=2,∠AEP=90°,且EP交正方形外角的平分线CP于点P,则PC的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)若该抛物线与x轴有公共点,求c的取值范围;
(Ⅱ)设该抛物线与直线![]() 交于M,N两点,若
交于M,N两点,若![]() ,求C的值;
,求C的值;
(Ⅲ)点P,点Q是抛物线上位于第一象限的不同两点,![]() 都垂直于x轴,垂足分别为A,B,若
都垂直于x轴,垂足分别为A,B,若![]() ,求c的取值范围.
,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形纸片OBCD的边OB在x轴上,OD在y轴上,点C在第一象限,且![]() .现将纸片折叠,折痕为EF(点E,F是折痕与矩形的边的交点),点P为点D的对应点,再将纸片还原。
.现将纸片折叠,折痕为EF(点E,F是折痕与矩形的边的交点),点P为点D的对应点,再将纸片还原。
(I)若点P落在矩形OBCD的边OB上,
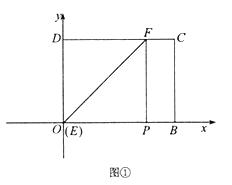
①如图①,当点E与点O重合时,求点F的坐标;
②如图②,当点E在OB上,点F在DC上时,EF与DP交于点G,若![]() ,求点F的坐标:
,求点F的坐标:
(Ⅱ)若点P落在矩形OBCD的内部,且点E,F分别在边OD,边DC上,当OP取最小值时,求点P的坐标(直接写出结果即可)。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示.下列结论:①方程=ax2+bx+c=0的两个根是x1=﹣1,x2=3:②a﹣b+c=0;③8a+c<0;④当y>0时,x的取值范围是﹣1<x<3;⑤当y随x的增大而增大时,一定有x<O.其中结论正确的个数是( )
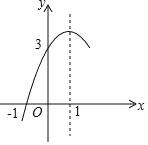
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
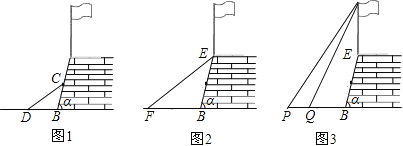
【题目】九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
备用数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com