
【题目】九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
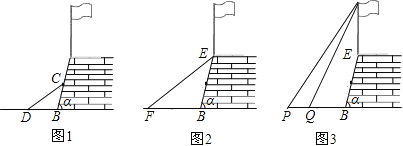
(1)如图1,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数.
(2)如图2,第二小组用皮尺量的EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米,请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
备用数据:![]() .
.
【答案】(1)76°;(2)3.8米;(3)5.7米.
【解析】
试题(1)根据∠α=2∠CDB即可得出答案.
(2)设EF的中点为M,过M作MN⊥BF,垂足为点N,过点E作EH⊥BF,垂足为点H,根据EH=2MN即可求出E点离地面FB的高度;
(3)延长AE,交PB于点C,设AE=x,则AC=x+3.8,CQ=x﹣0.2,根据![]() ,得出
,得出![]() ,求出x即可.
,求出x即可.
试题解析:解:(1)∵BD=BC,∴∠CDB=∠DCB.
∴∠α=2∠CDB=2×38°=76°.
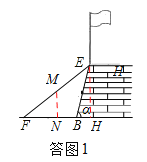
(2)如答图1,设EF的中点为M,过M作MN⊥BF,垂足为点N,过点E作EH⊥BF,垂足为点H,
∵MN∥AH,MN=1.9,∴EH=2MN=3.8(米).
∴E点离地面FB的高度是3.8米.
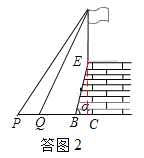
(3)如答图2,延长AE,交PB于点C,
设AE=x,则AC=x+3.8,
∵∠APB=45°,∴PC=AC=x+3.8.
∵PQ=4,∴CQ=x+3.8﹣4=x﹣0.2.
∵![]() ,
,
∴![]() ,解得
,解得![]() .
.
∴AE≈5.7(米).
答;旗杆AE的高度是5.7米.


科目:初中数学 来源: 题型:
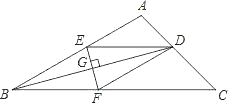
【题目】如图,在 ABC 中,BD 平分ABC 交 AC 于 D ,EF 垂直平分 BD ,分别交 AB, BC, BD于 E, F , G ,连接 DE, DF 。
(1)求证:四边形 BEDF 为菱形;
(2)若ABC 30, C 45, DE 4 ,求CF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=2
,EF=2![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
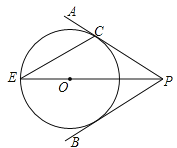
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )

A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=![]() (x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(1)求点D的坐标;
(2)点F是OC边上一点,若△FBC和△DEB相似,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
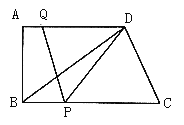
【题目】如图所示,在四边形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
(1)设△DPQ的面积为S,求S与t之间的函数关系式;
(2)分别求出出当t为何值时,①PD=PQ,②DQ=PQ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了培养学生的社会实践能力,今年“五一”长假期间要求学生参加一项社会调查活动.为此,小明在他所居住小区的600个家庭中,随机调查了50个家庭在新工资制度实施后的收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
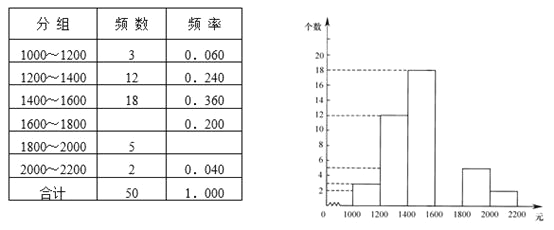
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布表和频数分布直方图;
(2)这50个家庭收入的中位数落在 小组;
(3)请你估算该小区600个家庭中收入较低(不足1400元)的家庭个数大约有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com