
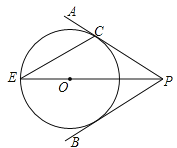
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
【答案】(1)证明见解析;(2)![]()
【解析】试题(1)连接OC,作OD⊥PB于D点.证明OD=OC即可.根据角的平分线性质易证;
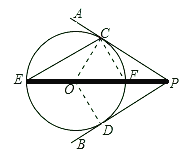
(2)设PO交⊙O于F,连接CF.根据勾股定理得PO=5,则PE=8.证明△PCF∽△PEC,得CF:CE=PC:PE=1:2.根据勾股定理求解CE.
试题解析:(1)证明:连接OC,作OD⊥PB于D点.
∵⊙O与PA相切于点C, ∴OC⊥PA.
(2)解:设PO交⊙O于F,连接CF.
∵OC=3,PC=4,∴PO=5,PE=8.
∵⊙O与PA相切于点C, ∴∠PCF=∠E.
又∵∠CPF=∠EPC, ∴△PCF∽△PEC,
∴CF:CE=PC:PE=4:8=1:2.
∵EF是直径, ∴∠ECF=90°.
设CF=x,则EC=2x.
则x2+(2x)2=62, 解得x=![]() .
.
则EC=2x=![]() .
.


科目:初中数学 来源: 题型:
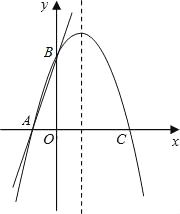
【题目】如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
(1)求抛物线的解析式;
(2)求抛物线的对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)求证:EM是⊙O的切线;
(2)若∠A=∠E,BC=![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() 和根号).
和根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
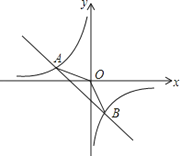
【题目】如图,在平面直角坐标系xOy中,一次函数y![]() =ax+b(a,b为常数,且a≠0)与反比例函数y
=ax+b(a,b为常数,且a≠0)与反比例函数y![]() =
=![]() (m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n).
(m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n).
(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知直线y=-![]() x+4与y轴交于A点,与x轴交于B点,C点坐标为(﹣2,0).
x+4与y轴交于A点,与x轴交于B点,C点坐标为(﹣2,0).
(1)求经过A,B,C三点的抛物线的解析式;
(2)如果M为抛物线的顶点,联结AM、BM,求四边形AOBM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。

(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
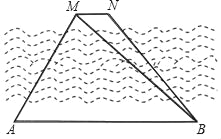
【题目】如图,在一条河的北岸有两个目标M、N,现在位于它的对岸设定两个观测点A、B.已知AB∥MN,在A点测得∠MAB=60°,在B点测得∠MBA=45°,AB=600米.
(1)求点M到AB的距离;(结果保留根号)
(2)在B点又测得∠NBA=53°,求MN的长.(结果精确到1米)
(参考数据:![]() ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com