
【题目】已知抛物线![]() .
.
(1)若该抛物线与x轴有公共点,求c的取值范围;
(Ⅱ)设该抛物线与直线![]() 交于M,N两点,若
交于M,N两点,若![]() ,求C的值;
,求C的值;
(Ⅲ)点P,点Q是抛物线上位于第一象限的不同两点,![]() 都垂直于x轴,垂足分别为A,B,若
都垂直于x轴,垂足分别为A,B,若![]() ,求c的取值范围.
,求c的取值范围.
【答案】(I)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)c的取值范围是
;(Ⅲ)c的取值范围是![]()
【解析】
(1) 抛物线与x轴有公共点,则判别式为非负数,列不等式求解即可;
(2)求出二次函数与直线的交点,并根据勾股定理求出MN的长度,列方程即可求解;
(3)由![]() 可知,P,Q两点的坐标特点,设坐标得到设点P的坐标为
可知,P,Q两点的坐标特点,设坐标得到设点P的坐标为![]() ,则点Q的坐标为
,则点Q的坐标为![]() ,代入二次函数,得到n,m的关系,则只需保证该方程有正根即可求解.
,代入二次函数,得到n,m的关系,则只需保证该方程有正根即可求解.
解:(I)∵抛物线![]() 与x轴有交点,
与x轴有交点,
∴一元二次方程![]() 有实根。
有实根。
![]() ,即
,即![]() .解得
.解得![]()
(Ⅱ)根据题意,设![]()
由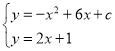 ,消去y,得
,消去y,得![]() ①.
①.
由![]() ,得
,得![]() .
.
∴方程①的解为![]()
![]()
![]() ,解得
,解得![]()
(Ⅲ)设点P的坐标为![]() ,则点Q的坐标为
,则点Q的坐标为![]() ,且
,且![]() ,
,
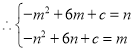 ,两式相减,得
,两式相减,得![]() ,即
,即![]()
![]() ,即
,即![]()
![]() ,其中
,其中![]()
由![]() ,即
,即![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,不合题意。
,不合题意。
又![]() ,得
,得![]() .
.
∴c的取值范围是![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() 的顶点为
的顶点为![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() .
.
(Ⅰ)若抛物线![]() 经过原点,求
经过原点,求![]() 的值;
的值;
(Ⅱ)是否存在![]() 的值,使得点
的值,使得点![]() 到
到![]() 轴距离等于点
轴距离等于点![]() 到直线
到直线![]() 距离的一半,若存在,请直接写出
距离的一半,若存在,请直接写出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)将![]() 的函数图象记为图象
的函数图象记为图象![]() ,图象
,图象![]() 关于直线
关于直线![]() 的对称图象记为图象
的对称图象记为图象![]() ,图象
,图象![]() 与图象
与图象![]() 组合成的图象记为
组合成的图象记为![]() .
.
①当![]() 与
与![]() 轴恰好有三个交点时,求
轴恰好有三个交点时,求![]() 的值:
的值:
②当![]() 为等边三角形时,直接写出
为等边三角形时,直接写出![]() 所对应的函数值小于0时,自变量
所对应的函数值小于0时,自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (b,c为常数)与x轴交于点
(b,c为常数)与x轴交于点![]() 和
和![]() ,与y轴交于点A,点E为抛物线顶点。
,与y轴交于点A,点E为抛物线顶点。
(Ⅰ)当![]() 时,求点A,点E的坐标;
时,求点A,点E的坐标;
(Ⅱ)若顶点E在直线![]() 上,当点A位置最高时,求抛物线的解析式;
上,当点A位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求b的值。
值最小时,求b的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳春三月,龙泉驿区的桃花又开了,小明乘坐地铁到龙泉看桃花,计划在龙平路地铁口下车,如图是龙平路地铁口的平面图,其有A、B、C、D四个出入口,小明任选一个出口下车出站,赏花结束后,任选一个入口入站乘车.
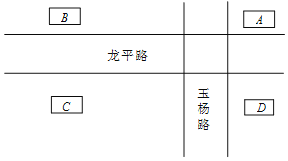
(1)小明从出站到入站共有多少种可能的结果?请用树形图或列表说明;
(2)求出小明从龙平路同一侧出入站的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组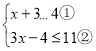
请结合题意填空,完成本题的解答:
(I)解不等式①,得_____________________;
(Ⅱ)解不等式②,得_________________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为____________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
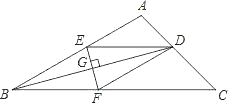
【题目】如图,在 ABC 中,BD 平分ABC 交 AC 于 D ,EF 垂直平分 BD ,分别交 AB, BC, BD于 E, F , G ,连接 DE, DF 。
(1)求证:四边形 BEDF 为菱形;
(2)若ABC 30, C 45, DE 4 ,求CF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 ;请结合题意填空,完成本题的解答.
;请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
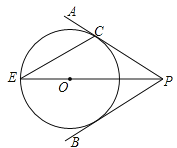
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com