
 在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.
在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.分析 (1)由CE=CF得∠CEF=∠CFE,因为∠CEF=∠B+∠EAB,∠CFE=∠ACD+∠CAE,欲证明∠CAE=∠BAE只要证明∠ACD=∠B即可.
(2)利用△ACD∽△ABC求出AB、BC,再证明EA=EB设EC=x,在RT△ACE中利用勾股定理即可求出x.
解答 解:(1)∵CE=CF,
∴∠CEF=∠CFE (等边对等角),
∵∠AFD=∠CFE(对顶角相等),
∴∠CEF=∠AFD(等量代换),
∵CD⊥AB∴∠ADF=90°(垂直定义),
在△AEC和△AFD中,∠ACE=∠ADF=90°,∠CEF=∠AFD,
∴180°-∠ACE-∠CEF=180°-∠ADF-∠AFD(三角形内角和定理),
即:∠CAE=∠EAD,
∴AE平分∠BAC(角平分线定义).
(2)在Rt△ADC中,∠ADC=90°,AC2=AD2+CD2,
∴$AC=\sqrt{A{D}^{2}+C{D}^{2}}=\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$,
∵∠CAD=∠BAC,∠CDA=∠ACB=90°,
∴△ACD∽△ABC(两角对应相等两三角形相似),
∴$\frac{AC}{AB}=\frac{AD}{AC}=\frac{CD}{BC}$(相似三角形对应边成比例)
∴$\frac{\sqrt{5}}{AB}=\frac{1}{\sqrt{5}}=\frac{2}{BC}$,
∴AB=5,BC=2$\sqrt{5}$,
∵EC=EF,
∴∠ECF=∠CFE=∠AFD,
∵∠B+∠ECF=90°,∠FAD+∠AFD=90°,
∴∠FAD=∠EBA(等角的余角相等),
∴EA=EB(等角对等边)
设EC=x,则EB=AE=2$\sqrt{5}$-x,
在RT△ACE中,∵AC2+CE2=AE2,
∴($\sqrt{5}$)2+x2=(2$\sqrt{5}$-x)2,
∴x=$\frac{3\sqrt{5}}{4}$.
∴CE=$\frac{3\sqrt{5}}{4}$.
点评 本题考查角平分线定义、等腰三角形的性质、相似三角形的判定和性质、勾股定理等知识,熟练掌握等腰三角形的性质是解题的关键,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
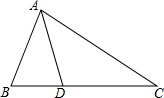 如图,在△ABC中,∠B=2∠C,AD平分∠BAC,AB=$6\sqrt{2}$,BD=$4\sqrt{2}$,则BC=$\frac{32\sqrt{2}}{3}$.
如图,在△ABC中,∠B=2∠C,AD平分∠BAC,AB=$6\sqrt{2}$,BD=$4\sqrt{2}$,则BC=$\frac{32\sqrt{2}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
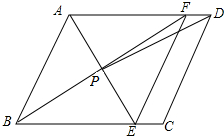 如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长2$\sqrt{7}$,四边形ABEF的面积8$\sqrt{3}$.
如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长2$\sqrt{7}$,四边形ABEF的面积8$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有一种足球是由32块黑白相间的牛皮缝制而成的,黑皮可看作正五边形,白皮可看作正六边形(正多边形为各边相等,各内角相等的几何图形),那么白皮、黑皮的块数为( )
有一种足球是由32块黑白相间的牛皮缝制而成的,黑皮可看作正五边形,白皮可看作正六边形(正多边形为各边相等,各内角相等的几何图形),那么白皮、黑皮的块数为( )| A. | 18、14 | B. | 16、16 | C. | 20、12 | D. | 22、10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com